1. Understanding the Work of a Constant Force

Work of F during the AB path
Consider a cube (the system) moving in a straight line from A to B.
A constant force F→ is applied to this cube.
The work of F→ during this movement
represents the contribution of this force (in terms of energy transfer) during the AB displacement.

How can we evaluate the work of this force?

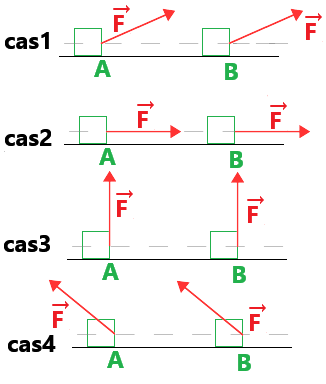
Work of F depending on its direction

The force F→ is oriented in four different ways.
Answer the following quiz (3 answers expected):

The force F→ does no work in the case:
The force F→ has maximum work in the case:
The work of the force F→ opposes the displacement in the case:

2. Definition of Work of a Force

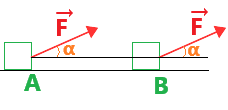
Work of a force definition
The work of a constant force F→ for a straight-line displacement AB→ of its application point is the dot product of F→ and AB→:

WAB(F→) = F→ . AB→ = F * AB * cosα

  • WAB(F→) : work expressed in Joules (J)
  • F : force value in Newtons (N)
  • AB : displacement length in meters (m)
  • α : angle between F→ and AB→ expressed in degrees or radians
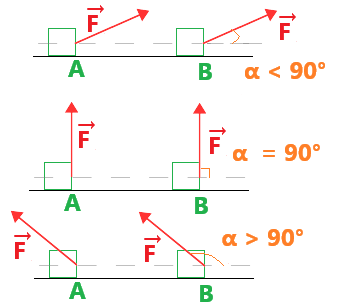
Work depending on the angle
Depending on the value of α, we have different types of work:
  • α < 90° : W > 0 → the work is positive (favors movement).
  • α = 90° : W = 0 → the work is zero.
  • α > 90° : W < 0 → the work is negative (opposes movement).

3. The Special Case of the Work Done by the Reaction Force

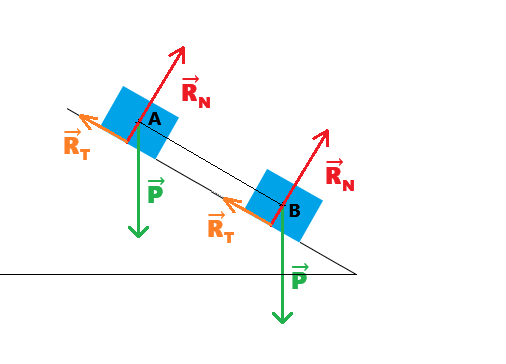
A box slides from A to B on an inclined plane.
Forces acting on the box:
  • Weight of the box P→
  • Reaction force of the inclined plane R→ (R→ = R→N + R→T)

    • What can we say about the work done by the reaction force?


    WAB(R→) = R→ . AB→ = R→N . AB→ + R→T . AB→
    R→N . AB→ = 0 because R→N and AB→ are perpendicular.
    R→T . AB→ = RT*AB*cos(180°) = -RT*AB

    Thus: WAB(R→) = -RT*AB

    Only the friction force (R→T) does work, opposing the motion.

    The work done by the friction force depends on the trajectory, making it a non-conservative force.

    4. The Special Case of the Work Done by Weight

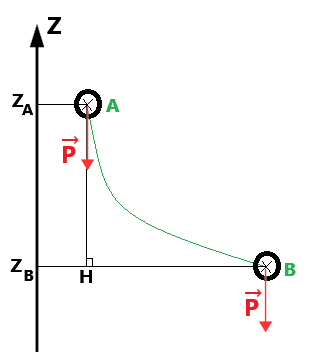
    work done by weight
    The system moves from A to B along an arbitrary trajectory.
    By definition, the work done by weight during the displacement is:
    WAB(P→) = P→ . AB→
    WAB(P→) = P→ . (AH→ + HB→)
    WAB(P→) = P→ . AH→ + P→ . HB→
    WAB(P→) = P→ . AH→ + 0 because P→ and HB→ are perpendicular.
    WAB(P→) = mg(ZA-ZB) because P=mg and P→ and AH→ are collinear.

    WAB(P→) = mg(ZA-ZB)

    The work done by weight does not depend on the trajectory, making weight a conservative force.

    5. The Kinetic Energy Theorem

    kinetic energy theorem

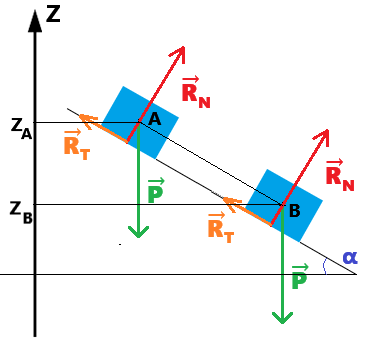
    According to the kinetic energy theorem:
    The variation in the kinetic energy of a system during a displacement AB
    is equal to the sum of the works of the forces applied to it during the displacement AB.


    ECB - ECA = ∑WAB(F→)
    • ECB = 1/2mvB², the final kinetic energy at B, expressed in Joules (J).
    • ECA = 1/2mvA², the initial kinetic energy at A, expressed in Joules (J).
    • ∑WAB(F→), the sum of the works of all forces, expressed in Newton (N).
    • vA and vB must be expressed in m/s.
    Let’s take the example of the box sliding from A to B. According to the kinetic energy theorem:
    ECB - ECA = ∑WAB(F→)
    1/2mvB² - 1/2mvA² = WAB(RT→) + WAB(P→)
    1/2mvB² - 1/2mvA² = -RT*((ZA-ZB)/sinα) + mg(ZA-ZB) because AB = (ZA-ZB)/sinα