1. Comprendre le travail d'une force constante

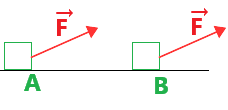
travail de F pendant le trajet AB
Soit un cube (le système) qui se déplace rectiligmement de A vers B.
On exerce sur ce cube une force constante F→.
Le travail de F→ au cours de se déplacement
représente la contribution de cette force (en terme de transfert d'énergie) au cours du déplacement AB.

Comment évaluer le travail de cette force?

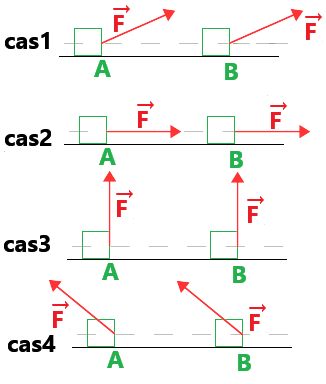
travail de F en fonction de sa direction

On oriente la force F→ de 4 manières différentes.
Répondez au Quizz suivant(3 réponses attendues):

La force F→ ne travaille pas dans le cas:
La force F→ a un travail maximal dans le cas:
Le travail de la force F→ s'oppose au déplacement dans le cas:

2. Définition du travail d'une force

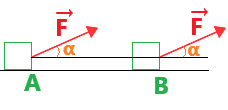
travail d'une force définition
Le travail d'une force constante F→ pour un déplacement rectiligne AB→ de son point d'application est le produit scalaire de F→ par AB→:

WAB(F→) = F→ . AB→ = F*AB*cosα

  • WAB(F→) : travail exprimé en Joules(J)
  • F : valeur de la force en Newton (N)
  • AB : longueur du déplacement en mètre (m)
  • α : angle entre F→ et AB→ exprimé en degré ou radian
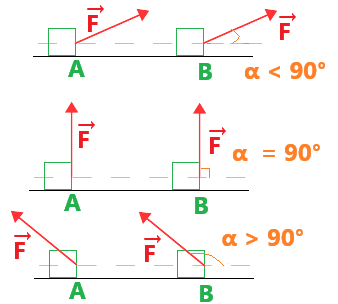
travail selon l'angle
Suivant la valeur de α, on a différents types de travail:
  • α < 90° : W > 0 le travail est moteur (favorise le mouvement).
  • α = 90° : W = 0 le travail est nul.
  • α > 90° : W < 0 le travail est résistant (s'oppose au mouvement).

3. Le cas particulier du travail de la force de réaction

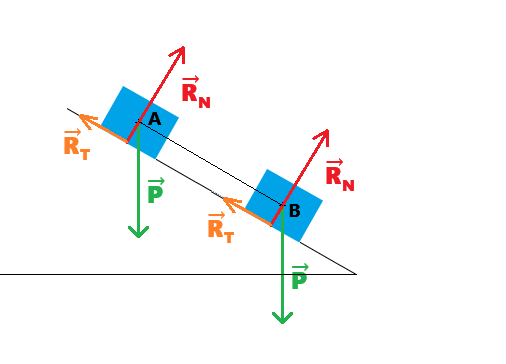
Une boîte glisse de A vers B sur un plan inclinée.
bilan des forces:
  • Poids de la boîte P→
  • Réaction du plan incliné R→ (R→ = R→N + R→T)

    • Que peut-on dire du travail de la force de réaction ?


    WAB(R→) = R→ . AB→ = R→N . AB→ + R→T . AB→
    R→N . AB→ = 0 car R→N et AB→ sont perpendiculaires.
    R→T . AB→ = RT*AB*cos(180°) = -RT*AB

    Donc : WAB(R→) = -RT*AB

    Seule la force de frottements (R→T) travaille, elle s'oppose au mouvement.

    Le travail de la force de frottements dépend de la trajectoire, c'est est une force non conservative.

    4. Le cas particulier du travail du poids

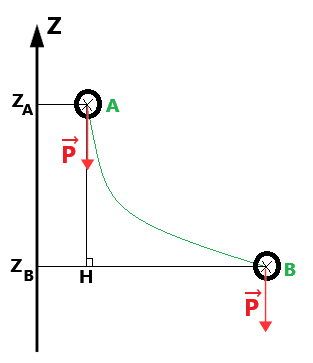
    travail du poids
    Le système se déplace de A vers B avec une trajectoire quelconque.
    Par définition le travail du poids au cours du déplacement est:
    WAB(P→) = P→ . AB→
    WAB(P→) = P→ . (AH→ + HB→)
    WAB(P→) = P→ . AH→ + P→ . HB→
    WAB(P→) = P→ . AH→ + 0 car P→ et HB→ sont perpendiculaires.
    WAB(P→) = mg(ZA-ZB) car P=mg et P→ et AH→ sont colinéaires.

    WAB(P→) = mg(ZA-ZB)

    Le travail du poids ne dépend pas de la trajectoire, le poids est une force conservative.

    5. Le théorème de l'énergie cinétique

    theoreme de l energie cinetique

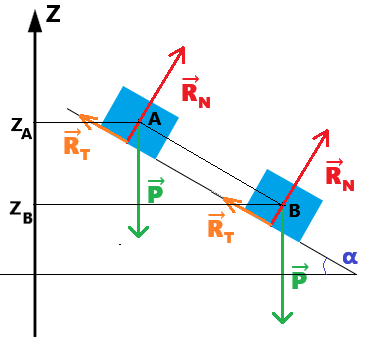
    D'après le théorème de l'énergie cinétique :
    La variation de l'énergie cinétique d'un système au cours d'un déplacemen AB
    est égale à la somme des travaux des forces exercées sur lui au cours du déplacement AB.


    ECB - ECA = ∑WAB(F→)
    • ECB = 1/2mvB², c'est l'énergie cinétique finale en B exprimée en Joules (J).
    • ECA = 1/2mvA², c'est l'énergie cinétique finale en B exprimée en Joules (J).
    • ∑WAB(F→), c'est la somme des travaux de toutes les forces exprimée en Newton (N).
    • vA et vB doivent être exprimées en m/s
    Prenons l'exemple ci-contre de la boîte qui glisse de A à B. D'après le théorème de l'énergie cinétique :
    ECB - ECA = ∑WAB(F→)
    1/2mvB² - 1/2mvA² = WAB(RT→) + WAB(P→)
    1/2mvB² - 1/2mvA² = -RT*((ZA-ZB)/sinα) + mg(ZA-ZB) car AB = (ZA-ZB)/sinα