1. Representing a Vector in a Coordinate System in Math and Physics

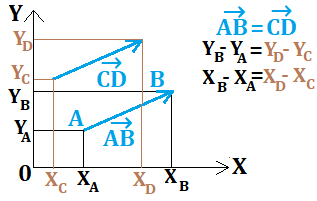
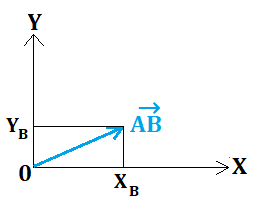
vector coordinates vector coordinates

In the coordinate system (O, X, Y), we have plotted points A (XA, YA) and B (XB, YB) as well as vector AB→ (XB-XA, YB-YA).
Key concept: my vector will have the same coordinates regardless of its position within the coordinate system.
In physics, if I am only interested in the coordinates of a force, I can position it anywhere in my coordinate system,

The easiest place is at the origin since XA = YA = 0, so AB→ becomes (XB, YB)

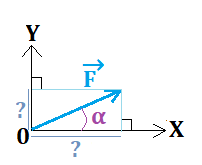
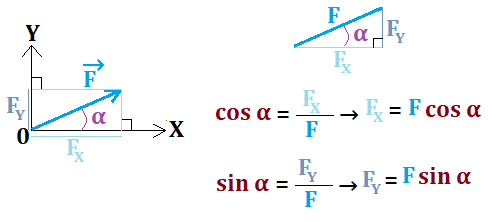
vector coordinates
vector coordinates
In general, we rarely work with point coordinates directly. For us, a vector may represent a force,
and we know its value proportional to its length and inclination α relative to the horizontal (see diagram).
When a physicist needs the coordinates of F→, they orthogonally project the vector onto X and then onto Y.
If FX and FY are the coordinates of F→(FX, FY), these three lengths (F, FX, and FY) form a right triangle.
    In a right triangle:
  • cos α = adjacent side/hypotenuse and sin α = opposite side/hypotenuse
  • So: F→ (FX, FY) → F→ (Fcos α, Fsin α)
      • A practical example if F = 12.0N and α = 30.0°:
    • cos(30.0°) = 0.866 and sin(30.0°) = 0.500
    • FX = Fcos(30.0°) + 12.0 x 0.866 = 10.4N
    • FY = Fsin(30.0°) + 12.0 x 0.500 = 6.00N
    • F→ (10.4, 6)

2. Mastering the Right Triangle

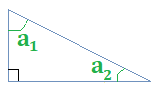
right triangle
In a right triangle, knowing a1 or a2 gives you all the angles,
In a triangle, the sum of the angles equals 180°, so: a1 + a2 + 90 = 180, thus knowing a1 or a2 gives you all angles.
    For instance, if a1 = 20°:
  • a1 + a2 + 90 = 180
  • a1 + a2 = 90
  • a2 = 90 - a1 = 90 - 20 = 70°
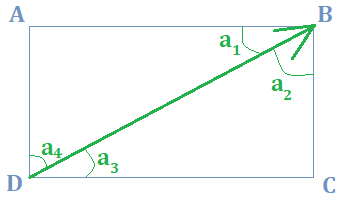
right triangle
When working with forces, it is important to "play" with right triangles and angles.
In the example on the left, a1 = 25°.
  • For triangle ABD, the sum of the angles = 180°:
    • a1 + a4 + 90 = 180
    • a4 = 90 - a1 = 90 - 25 = 65°
  • At B, the angle is right: a1 + a2 = 90° → a2 = 90 - a1 = 65°
  • At D, the angle is right: a3 + a4 = 90° → a3 = 90 - a4 = 25°
  • Note: since triangles ABD and CDB are congruent, we necessarily have a1 = a3 and a2 = a4
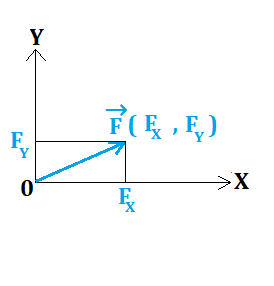
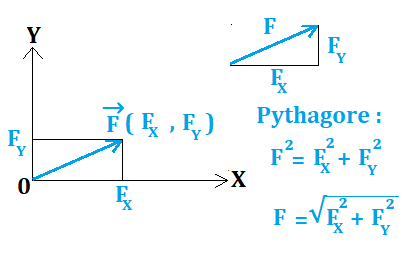
right triangle2 right triangle3
If I know the coordinates of F→ (FX and FY)
To find the value of the force F→, simply use the Pythagorean theorem (see diagram).
    An example: say FX = 4N and FY = 3N
  • F = √(F²X + F²Y) = √(4² + 3²)
  • F = √25 = 5N

3. Did you understand how to find the coordinates of a force?

A small random quiz: you must select the correct coordinates of vector F→ (FX, FY).
quiz progress: 1 / 8 CORRECT: 0 INCORRECT: 0
FX:
FY:

4. Applying a Vector Equality in Physics

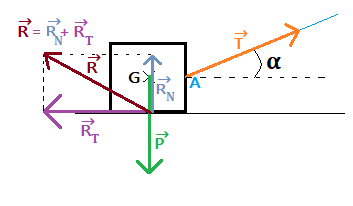
cube on the ground
cube on the ground

A cube is placed on the ground. We attach a string at A and move the cube along the ground at a constant speed.
We study the cube, choosing it as our system in the Earth's reference frame.

  • P→: Weight of the cube exerted by the Earth
  • T→: Tension of the string (exerted by the string)
  • R→: Ground reaction force (exerted by the ground), which can be decomposed into:
    • RT→: Frictional force or tangential reaction
    • RN→: Normal reaction (perpendicular)
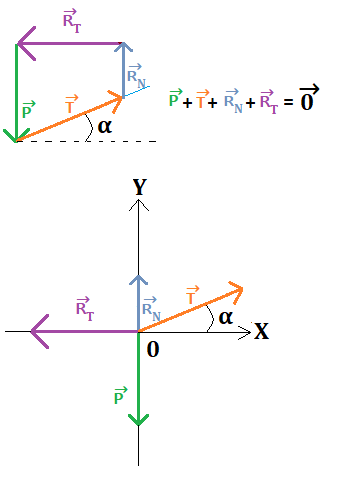
cube on the ground
If the motion is linear and uniform, according to the principle of inertia: P→ + T→ + R→N + R→T = 0→
This vector equation cannot be directly exploited; the key is to define a coordinate system and work with the components!

The vector equality written above holds in all directions of our coordinate system.
In this 2D example, we get two equations, but in a 3D context, we would have three!

    The forces have coordinates: P→ (PX, PY), T→ (TX, TY), R→N (RNX, RNY), R→T (RTX, RTY):
  • Along the X-axis: PX + TX + RNX + RTX = 0
  • Along the Y-axis: PY + TY + RNY + RTY = 0

Of course, you must specify the coordinates PX, TX, PY, etc., but that's the method!
To make things simpler, I’ve aligned the origins of my vectors with the origin of my coordinate system.
Now that you know how to find the coordinates of forces (see section 3), you can find the correct equations!

It's your turn: for each vector, click on the two correct coordinates.

PX :
PY :
TX :
TY :
RNX :
RNY :
RTX :
RTY :

Your equations:

Along the X-axis: + + + = 0
Along the Y-axis: + + + = 0
reaction force

These two equations allow us to obtain valuable values, for example:

    We have measured:
  • the mass of the cube: m = 2.00 kg (we'll use g = 9.81 N/kg), thus: P = mg = 2 x 9.81 = 19.6 N
  • the angle α: 20.0°
  • the tension of the string T→, T = 25.0 N

Using our equations, we can determine the reaction force R→:

  • 0 + Tcosα + 0 - RT = 0, so RT = Tcosα = 25cos(20°) = 23.5 N
  • -P + Tsinα + RN + 0 = 0, so RN = P - Tsinα = 19.6 - 25sin(20°) = 11.0 N
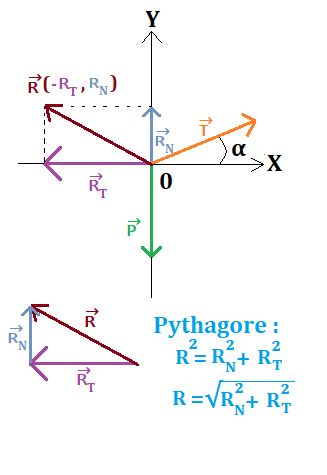
  • We have the coordinates of R→ (-RT, RN), that is, R→ (-23.5, 11)
  • The value of R according to the Pythagorean theorem: R = √(R²N + R²T) = √(23.5² + 11²) = 25.9 N