1. Représenter un vecteur dans un repère en mathématique et en physique

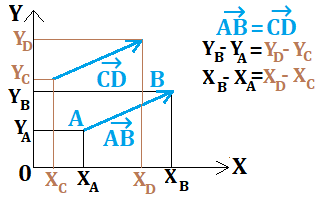
coordonnées d'un vecteur coordonnées d'un vecteur

On a représenté dans le repère (O, X, Y) les points A (XA, YA) et B (XB, YB) ainsi que le vecter AB→ (XB-XA, YB-YA).
Ce qu'il faut bien comprendre: mon vecteur aura les mêmes coordonnées quelque soit sa position dans mon repère.
En physique, si je m'intéresse uniquement aux coordonnées de ma force, je peux la représenter où je veux dans mon repère,

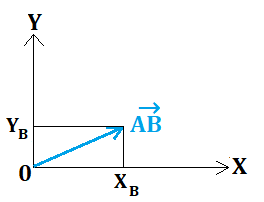
Le plus simple c'est de partir de l'origine, vu que XA = YA = 0, on a alors AB→ (XB, YB)

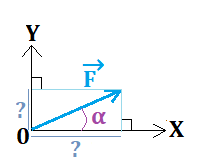
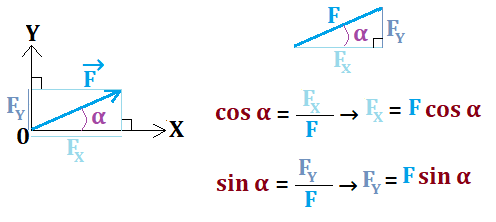
coordonnées d'un vecteur
coordonnées d'un vecteur
En fait, on va rarement travailler avec des coordonnées de points, pour nous, un vecteur représente par exemple une force,
on connait sa valeur qui est proportionnelle à sa longueur et son inclinaison α par rapport à l'horizontal (voir schéma).
Lorsque le physicien veut les coordonnées de F→ il doit projeter orthogonalement son vecteur sur X puis sur Y.
Si FX et FY sont les coordonnées de F→(FX, FY), ces 3 longueurs (F, FX et FY) forment un triangle rectangle.
    Dans un trianfle rectangle:
  • cos α = côté adjacent/hypothénuse et sin α = côté opposé/hypoténuse
  • Donc : F→ (FX, FY) → F→ (Fcos α, Fsin α)
      • Un exemple concret si F = 12.0N et α = 30.0°:
    • cos(30.0°) = 0.866 et sin(30.0°) = 0.500
    • FX = Fcos(30.0°) + 12.0 x 0.866 = 10.4N
    • FY = Fsin(30.0°) + 12.0 x 0.500 = 6.00N
    • F→ (10.4, 6)

2. Maîtriser le triangle rectangle

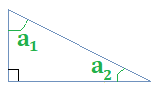
triangle rectangle
Dans un triangle rectangle, il suffit de connaitre a1 ou a2 pour connaitre tous les angles,
Dans un triangle, la somme des angles est égale à 180° , ainsi : a1 + a2 + 90 = 180, du coup connaitre a1 ou a2, c'est connaitre tous les angles.
    par exemple si a1 = 20°:
  • a1 + a2 + 90 = 180
  • a1 + a2 = 90
  • a2 = 90 - a1 = 90 - 20 = 70°
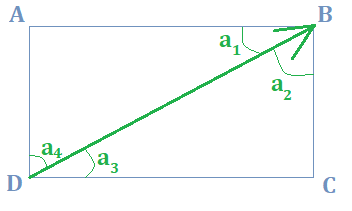
triangle rectangle
Lorsque l'on travail avec des forces, il faut savoir "jouer" avec les triangles rectangles et les angles.
Dans l'exemple à gauche, a1 = 25°,
  • Pour le triangle ABD la somme des angles = 180° :
    • a1 + a4 + 90 = 180
    • a4 = 90 - a1 = 90 - 25 = 65°
  • En B l'angle est droit : a1 + a2 = 90° → a2 = 90 - a1 = 65°
  • En D l'angle est droit : a3 + a4 = 90° → a3 = 90 - a4 = 25°
  • Remarque: comme les triangles ABD et CDB sont superposables, on a forcément a1 = a3 et a2 = a4
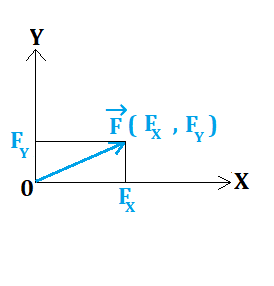
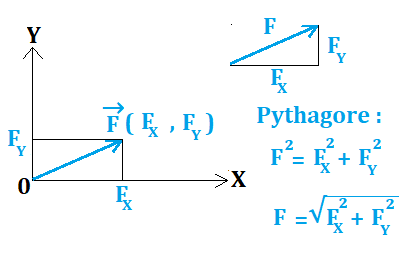
triangle rectangle2 triangle rectangle3
Si je connais les coordonnées de F→ (FX et FY)
Pour trouver la valeur de la force F→, il suffit d'utiliser le théorême de Pythagore (voir schéma).
    Un exemple : disons que FX = 4N et FY = 3N
  • F = √(F²X + F²Y ) = √( 4² + 3² )
  • F = √25 = 5N

3. Avez-vous bien compris comment trouver les coordonnées d'une force?

Un petit quiz aléatoire, vous devez sélectionner les bonnes coordonnées du vecteur F→ (FX, FY).
progression du quiz : 1 / 8 JUSTE : 0 FAUX : 0
FX :
FY :

4. Exploiter une égalité vectorielle en physique

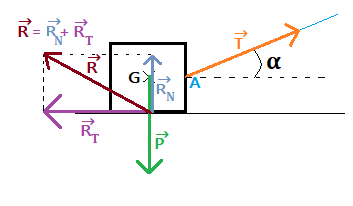
cube posé sur le sol
cube posé sur le sol

Un cube est posé sur le sol, on attache un fil en A et on déplace le cube sur le sol à vitesse constante.
On étudie le cube, donc on le choisit comme système dans le référentiel Terrestre.

  • P→ : Poids du cube exercée par la Terre
  • T→ : Tension du fil (exercée par le fil)
  • R→ : Réaction du sol (exercée par le sol), R→ peut être décomposée:
    • RT→ : forces de frottement ou réaction tangentielle
    • RN→ : réaction normale (perpendiculaire)
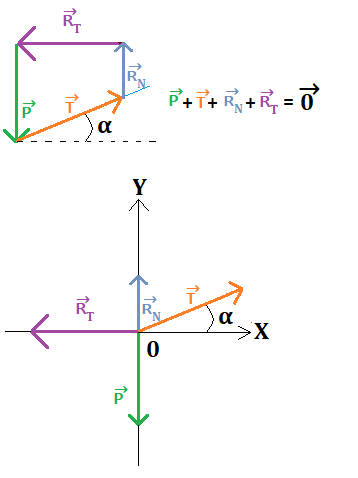
cube posé sur le sol
Si le mouvement est rectiligne uniforme, d'après le principe d'inertie : P→ + T→ + R→N + R→T = 0→
On ne peut pas exploiter directement cette relation vectorielle, la clé c'est de définir un repère et de travailler avec les coordonnées!

L'égalité vectorielle écrite ci-dessus est vrai dans toutes les directions de mon repère.
Ici je vais obtenir 2 équations car le mouvement est en 2D mais avec un mouvement en 3D, j'aurais 3 équations!

    Les forces ont pour coordonnées : P→ (PX,PY) , T→ (TX,TY) , R→N (RNX,RNY) , R→T (RTX,RTY) :
  • Selon l'axe X : PX + TX + RNX + RTX = 0
  • Selon l'axe Y : PY + TY + RNY + RTY = 0

Bien sûr, il faut expliciter les coordonnées PX, TX, PY , ect... mais c'est la méthode!
Pour que se soit plus simple, j'ai fais coïncider l'origine de mes vecteurs avec l'origine de mon repère.
Maintenant que vous savez trouver les coordonnées des forces (voir 3.), vous êtes capables de trouver les bonnes équations!

C'est à vous de jouer, pour chaque vecteur il faut cliquer sur les 2 bonnes coordonnées.

PX :
PY :
TX :
TY :
RNX :
RNY :
RTX :
RTY :

Vos équations:

Selon l'axeX : + + + = 0
Selon l'axeY : + + + = 0
force de réaction

Ces 2 équations permettent d'obtenir de précieuses valeurs, par exemple:

    On a mesuré:
  • la masse du cube : m = 2,00 kg (on prendra g = 9,81 N/kg) du coup: P = mg = 2x9.81 = 19.6N
  • l'angle α : 20,0°
  • La tension du fil T→, T = 25,0N

Grâce à nos équations, on peut déterminer la force de réaction R→:

  • 0 + Tcosα + 0 - RT = 0 donc RT = Tcosα = 25cos(20°) = 23.5N
  • -P + Tsinα + RN + 0 = 0 donc RN = P - Tsinα = 19.6 -25sin(20°) = 11,0 N
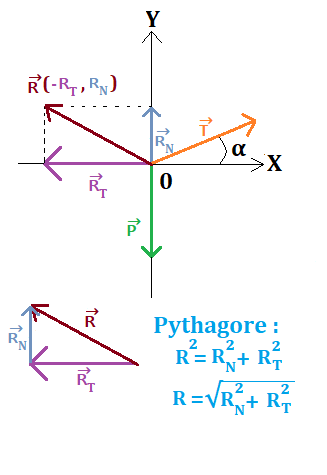
  • On a les coordonnées de R→ (-RT, RN) soit R→ (-23.5, 11)
  • La valeur de R → d'après le théorême de Pythagore: R = √(R²N + R²T) = √(23.5² + 11²) = 25.9N