The Proportions Game (2025)
Back to home1. Why this game?
"Two numbers a and b are proportional if one can be obtained by multiplying or dividing the other by a coefficient k, called the coefficient of proportionality."The concept of proportion is linked to multiplication and division and should be learned together. Unfortunately, this is rarely the case.
To win this game, you will need to master the following concepts:
- multiplication, division, proportion, and the link between them
- mental math
- explore different possibilities to find the best one
2. How to play?
The goal of the game is to buy as many 🍅, 🍆, or 🍓 as possible with a certain number of 🟡 based on a certain price, for example 3🟡/🍓.
Mathematically, the price represents the proportion between the number of 🟡 and the number of 🍓.
The number of 🍓 must be a whole number.
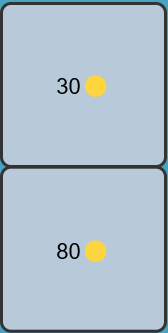
- You get 🟡 by selecting a "Gold" card (see 2 Gold cards on the right).
- The number of 🟡 must allow you to buy a whole number of 🍆, otherwise, it's game over!
- For example, if the price is 4🟡/🍆:
- I can use the 80🟡 card, because 80/4 = 20, so I win 20🍆.
- But if I try to use the 30🟡 card, I lose the game because 30/4 is not a whole number, 30/4 = 7.5.
- However, I have a way to modify the value of 🟡 on the card! (see below)
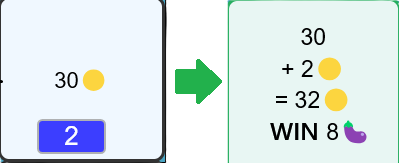
- You have a certain number of "Gold" available at the beginning of the game that you can add to the value on the card.
- You need to drag and drop a number onto the card to modify the number of 🟡 and use the card.
- In the example on the left, with 32🟡 and a price of 4🟡/🍆, I can buy 8🍆 because 32/4 = 8.
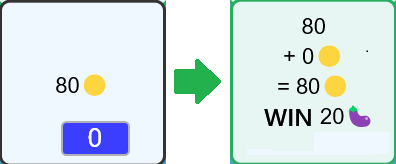
- To use a Gold card without changing the value on the card, you need to drag and drop the number 0.
The game may have several rounds depending on the difficulty. If the player hasn't managed to get the maximum number of 🍆 by the end of the round, it's game over.😱
So, you need to think carefully about the best way to distribute the available Gold at the start of each round to win.
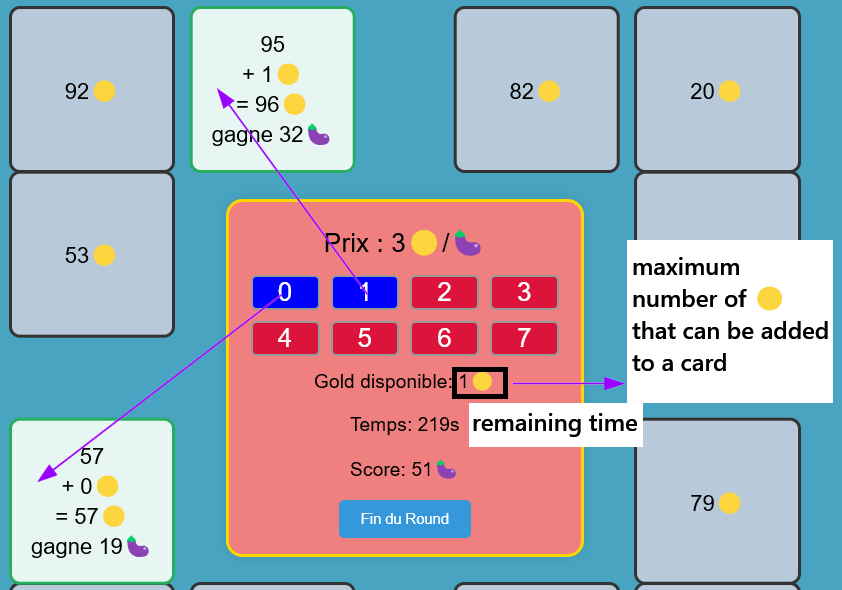
Are you ready to take on the challenge?