Weight

1. Example of Force: Weight

A mechanical action (pushing someone, attraction of a magnet...) is modeled by a force.
A force is represented by an arrow (i.e., a vector).
If I speak of the object under study: a pen, a car, the Earth... We will use the word system.
Let's detail the notion of force by taking as an example the weight of an object called a system.

• The vector (or arrow) weight is denoted P→.


• A force has 4 characteristics:
  1. Point of application → where the force is exerted
  2. Direction → it's the "line of action": vertical, horizontal, 30° relative to the horizontal...
  3. Sense → it's the orientation of the direction: upward, downward, to the right....
  4. Value → it's expressed in Newtons (N)


• For the weight P→ of a system, the characteristics are:
  1. Point of application → center of gravity of the system
  2. Direction → vertical
  3. Sense → downward
  4. Value → it's given by the weight formula P = mg.
     • P: weight of the system in Newtons (N)
     • m: mass of the object in kilograms (kg)
     • g: acceleration due to gravity g = 9.81 N/kg

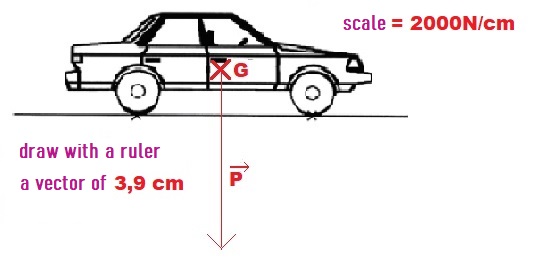
2. An Example: Calculating and Representing the Weight of a Car with a Mass of 0.8 tonne.

• We need to calculate the value of the weight P which we don't know.
  • P = mg = 800 x 9.81 = 7848 N (1 tonne = 1000 kg so 0.8t = 800 kg)
• To represent the weight, we need to choose a scale (in N/cm) and calculate the length of the corresponding vector.
• With the scale 2000N/cm: length = 7848 / 2000 = 3.9 cm
• We can now represent vector P→ with the scale 2000N/cm