Optique géométrique 👓
1. Les sources lumineuses

- La lumière est due à des processus énergétiques :
- le Soleil → l'énergie provient de la fusion de 4 noyaux d'Hydrogène pour former un noyau d'Hélium
- le feu → l'énergie est d'origine thermique
- la lampe → l'énergie est d'origine électrique
Tous les objets éclairés qui renvoient la lumière sont des sources secondaires.
C'est majoritairement via des sources secondaires que nous voyons.
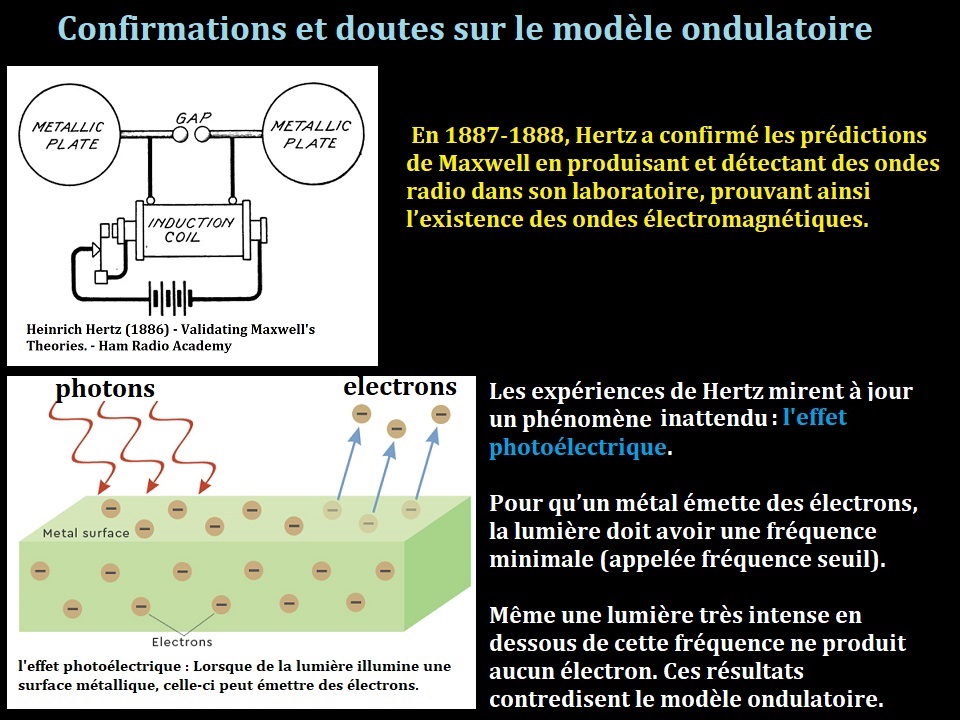
La flamme de la bougie ou une étoile lointaine peut être considérée comme une source ponctuelle,
car elle est petite par rapport à sa distance au point d'observation.
Les sources ponctuelles émettent de la lumière également dans toutes les directions.
2. Le modèle du rayon lumineux
,
la lumière se propage rectilignement à la vitesse de 3 x108 m/s (dans l'air ou le vide),
on peut donc la modéliser par des rayons.
Elle permet d'expliquer une bonne partie de ce que l'on observe au quotidien.
Par contre, elle ne permet pas d'expliquer un phénomène comme l'arc-en-ciel 🌈.
Quelque chose me semble faux sur l'image de droite,
En réalité, on va juste voir la zone éclairée sur l'écran :
On ne voit pas directement la lumière mais ce qu'elle éclaire.
Donc le rayon lumineux n'est qu'une abstraction mathématique,
d'où le nom d'optique géométrique !

3. Voir des objets ?

Il est légitime d'être surpris en se voyant derrière un miroir pour la 1ère fois ou qu'une paille intacte semble cassée.
Ces 2 images illustrent une idée simple, que l'on a tendance à oublier :
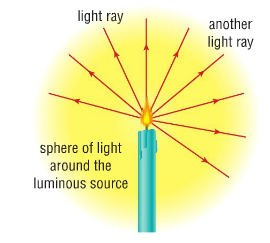
L'œil n'a pas un accès direct aux objets, il a accès à la lumière reçue par la rétine.
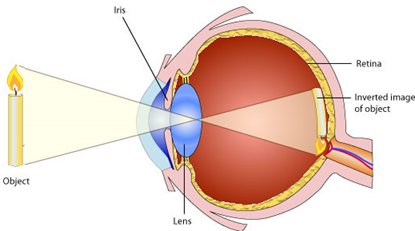
- L'image (retournée par le cristallin) se forme sur la rétine.
- Des cellules nerveuses convertissent la lumière en signaux électriques
- Les signaux électriques sont envoyés au cerveau via le nerf optique
- Le cerveau va interpréter les signaux électriques pour former l'image.
4. Le rôle de l'interprétation
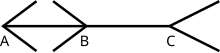
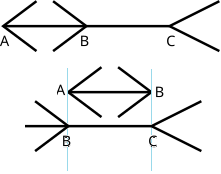
Il s'agit de l'illusion de Müller-Lyer, elle s'explique en considérant la perception spatiale du cerveau.
Il associe les flèches > < à des objets qui s'éloignent et les flèches < > à des objets qui se rapprochent,
d'où la différence de longueur perçue.

Il y a autant de rectangles que de cercles !!
Les cercles sont entre les rectangles.
Normalement, le cerveau choisit de ne pas les voir.
Lorsqu'il analyse l'image, "il se dit" :
C'est une image en 3D, donc les cercles n'existent pas, c'est un effet de perspective.

-
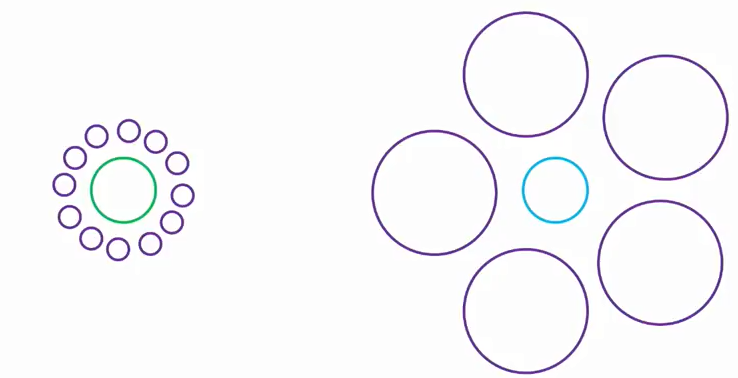
Le cercle de gauche semble plus grand que celui de droite, car :
- le cercle de gauche est entouré de petits cercles
- le cercle de droite est entouré de grands cercles
- On juge de la taille des objets par contraste
- Même si on sait que les cercles sont de même taille,
notre perception reste influencée par le contexte

Elle représente un mur, un cigare y est planté, perpendiculairement au mur.
Une fois qu'on a vu le cigare, l'illusion disparaît,
le cerveau a changé son interprétation.
Kokichi Sugihara est un chercheur et professeur japonais,
connu pour ses travaux en illusion visuelle et en perception spatiale.
La flèche reste orientée vers la droite, c'est de la magie !
Ce phénomène repose sur la manipulation subtile des propriétés géométriques
et de la perception bidimensionnelle vs tridimensionnelle.
La taille et la position des différentes parties de la flèche sont telles que notre cerveau "lisse" le changement,
nous donnant l'illusion que la flèche reste orientée de la même façon, même après une rotation.
Pour conclure, on voit avec nos yeux/cerveau, c'est un "capteur" actif qui interprète l'information.
Cette illusion ne serait pas possible si on regardait directement l'objet avec nos yeux,
car contrairement à une caméra qui forme une image plate, on est capable de voir en 3D...
5. Voir avec 2 yeux

Parce que le cerveau a appris à fusionner les 2 images ! On appelle ça... la fusion visuelle.
L'angle étant légèrement différent, le cerveau reçoit 2 images légèrement décalées,
il est capable d'utiliser ce décalage pour former une image tridimensionnelle.
Lorsqu'on ferme un œil, on remarque un léger changement : c'est le passage de la 3D à la 2D.
A la naissance, un bébé voit double. Il lui faut environ 6 mois pour voir correctement en 3D.
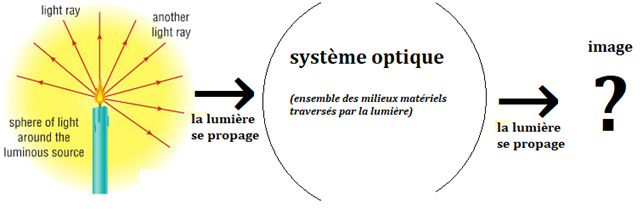
Si je trace plusieurs rayons de la flamme jusqu'à son image...
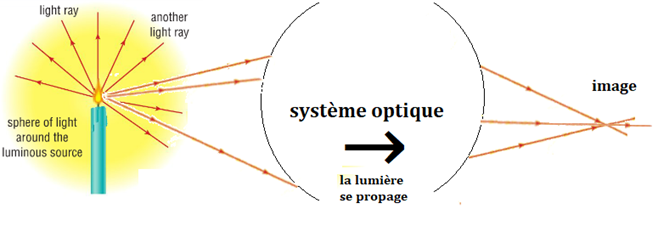
Tous les rayons lumineux issus de ma source doivent se croiser au point image.
L'image est la zone de l'espace où les rayons issus de l'objet convergent.
Ok pour l'image d'une source ponctuelle, mais...
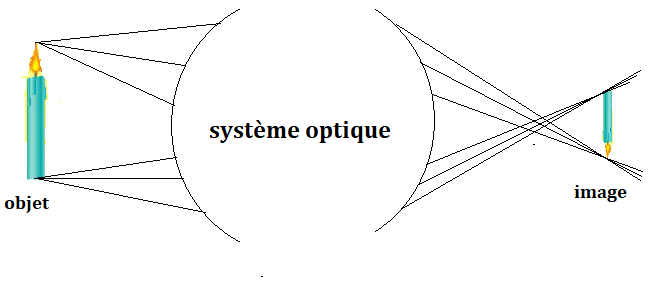
- On part du principe que l'image peut être :
- agrandie
- réduite
- inversée
- mais pas déformée !
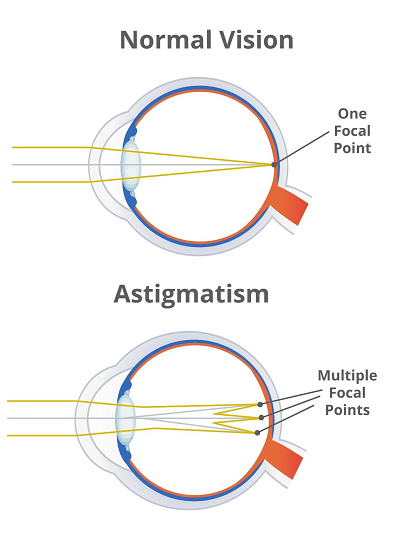
C'est le cas lorsque l'œil est astigmate, cela signifie qu'il a une forme irrégulière dans ses structures optiques,
principalement dans la cornée (ou parfois dans le cristallin),
ce qui fait que les rayons lumineux ne sont pas focalisés correctement en un seul point sur la rétine.
Au lieu de cela, l'œil astigmate produit une image déformée, souvent sous forme de taches floues ou de lignes étendues.
De la même façon, les systèmes optiques sont stigmates ou astigmates.
-
On travaillera avec des systèmes optiques stigmates :
- tous les rayons lumineux provenant d'une source ponctuelle se croisent en un seul point
- il n'y a pas de déformation de l'image.
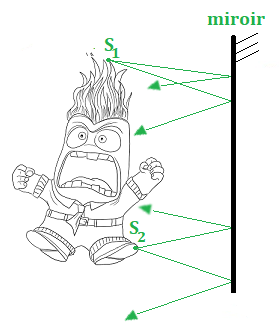
Le miroir est un système optique stigmate.
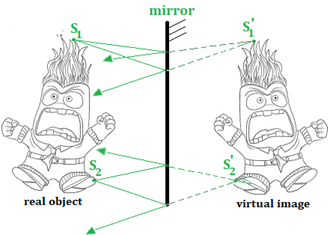
Pour représenter l'image par le miroir de mon bonhomme,
je cherche les images de 2 sources, S1 et S2
Les rayons lumineux divergent (ils s'écartent).
Donc, aucune chance qu'ils se croisent !
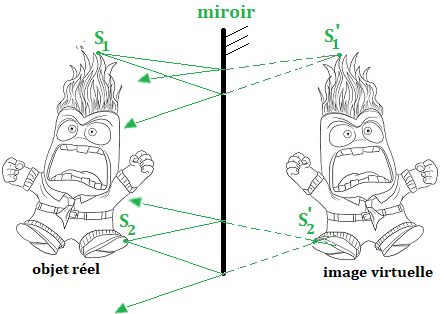
ce qui compte ce sont les rayons lumineux qui arrivent sur la rétine.
Les rayons issus de S1 semblent provenir de S'1
On peut voir S'1 avec un capteur (caméra, œil...) situé au niveau de l'objet,
mais si on place un écran en S'1, on ne voit rien, puisqu'aucun rayon ne parvient jusque là.
C'est une image virtuelle, on peut la voir mais elle n'existe pas.
Pour la trouver graphiquement, il faut prolonger les rayons réfléchis.
1. Loi de la réflexion
-
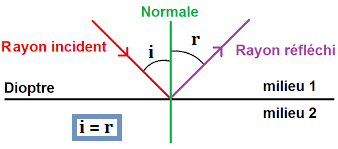
Le vocabulaire est important ici :
- Le dioptre : c'est la surface qui sépare deux milieux différents.
- La normale : c'est la perpendiculaire au dioptre,
les angles sont mesurés par rapport à la normale. - Le rayon incident : c'est le rayon qui "arrive" sur le dioptre.
- i : c'est l'angle d'incidence.
- r : c'est l'angle de réflexion.
D'après la loi de la réflexion : i = r
Comme nous l'avons vu au III, l'image d'un objet dans un miroir est une image virtuelle.Géométriquement, le miroir est un axe de symétrie entre l'objet et l'image.
Seul le miroir plan est stigmatique ; un miroir sphérique est astigmatique (miroirs déformants).
2. Loi de la réfraction

Donc, les parties sous l'eau et dans l'air arrivent sur la rétine avec des angles différents.
La lumière est déviée lorsqu'elle change de milieu,
c'est le phénomène de réfraction.
-
La vitesse de la lumière dépend du milieu traversé : c = c0/n
- c : vitesse de la lumière dans le milieu considéré
- c0 = 3,00 × 108, c'est la vitesse de la lumière dans l'air ou le vide.
- n : indice de réfraction du milieu transparent, par exemple :
- Dans l'air : nair = 1 → cair = c0/nair = 3,00 × 108 m/s
- Dans l'eau : neau = 1,3 → ceau = c0/neau = 3,00 × 108/1,3 = 2,31 × 108 m/s
- Dans le verre : nverre = 1,5 → cverre = c0/nverre = 3,00 × 108/1,5 = 2,00 × 108 m/s
son parcours est celui qui s'effectue en un minimum de temps.
Supposons que la lumière (à droite) se propage de A à B,
en traversant l'air puis le verre.
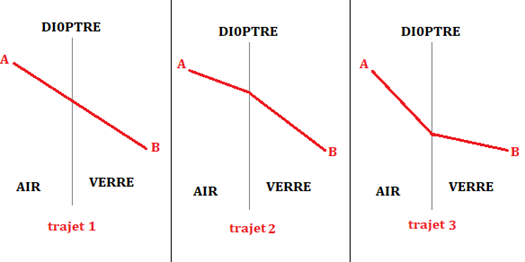
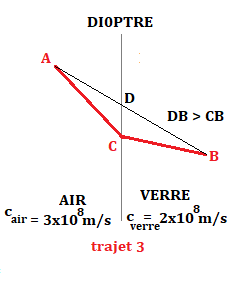
Étant donné que la vitesse de la lumière dans le verre est plus faible que dans l'air (cverre = 2,00 × 108 m/s et cair = 3,00 × 108 m/s),
pour avoir le temps de parcours minimum, il vaut mieux réduire la distance parcourue dans le verre, et pour cela, le rayon doit être dévié !
Puisque la vitesse de la lumière dépend de l'indice de réfraction,
le principe de Fermat implique une relation entre les indices et les angles : c'est la loi de la réfraction.
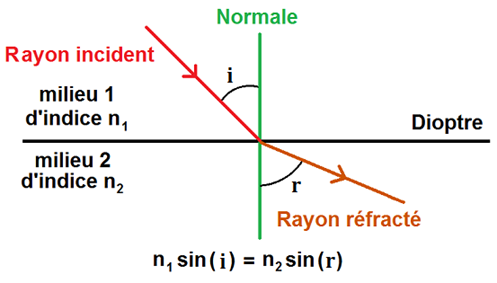
-
Loi de la réfraction : n1sin(i) = n2sin(r)
- i : angle incident
- r : angle réfracté
- n1 : indice de réfraction du milieu 1
- n2 : indice de réfraction du milieu 2
Les rayons sont déviés de telle sorte que la distance parcourue dans le milieu 1 est raccourcie par rapport à la ligne droite.
La vitesse est donc plus faible dans le milieu 1. Comme c = c0/n (c et n sont inversement proportionnels),
l'indice de réfraction n1 est le plus grand, donc n1 > n2.
La réponse du mathématicien :
r > i → sin(r) > sin(i), car x → sin(x) est une fonction croissante.
Puisque n1sin(i) = n2sin(r) et sin(r) > sin(i), on a forcément n1 > n2.
3. La 3ème loi de Snell-Descartes
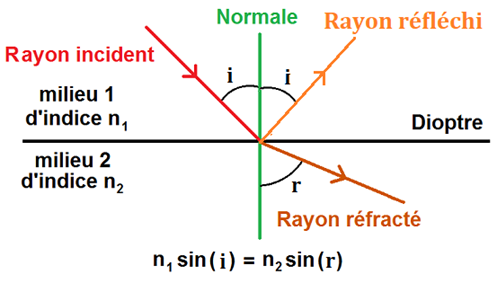
mais une partie de l'énergie lumineuse est aussi réfléchie.
D'après la 3ème loi de Snell-Descartes:
le rayon réfléchi, le rayon incident le rayon réfracté et la normale au dioptre sont dans le même plan.
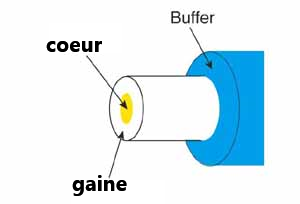
mais il existe également des fibres en plastique pour certaines applications spécifiques.
L'information est codée en signaux lumineux (0 : pas de lumière, 1 : lumière) qui se propagent dans le cœur.
Mais si la gaine est en plastique ou en verre (donc transparent),
Faites varier l'angle d'incidence i de 0 à 90° en déplaçant le petit carré bleu vers la gauche.
Si i augmente, à un moment donné r = 90° alors que i < 90°, si on continue à augmenter i...
r > 90° n'est pas possible : ce n'est plus une réfraction, mais une réflexion.
C'est la réflexion totale interne.
De cette façon, la lumière reste confinée dans le cœur de la fibre.
Si i est supérieur à l'angle critique (ou limite) °, on a une réflexion.
- Aide :
- Si on a par exemple sin(i) = 0,5, pour trouver l'angle i,
on peut utiliser la fonction arcsin (fonction inverse de sin)
soit i = arcsin(sin(i)) = arcsin(0,5) = 30°.
D'après la loi de Descartes : n1sin(i) = n2sin(r).
Comme sin(r) = sin(90°) = 1, on a : n1sin(i) = n2.
- Soit : sin(i) = n2/n1
- i = arcsin(n2/n1)
Pour transporter l'information sur de longues distances, il faut éviter les pertes.
Malheureusement, à chaque réflexion, une infime partie de l'intensité lumineuse est perdue.
On peut facilement restreindre le nombre de réflexions.
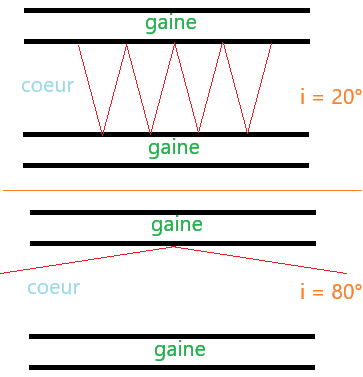
on constate que plus i est grand et proche de 90°, moins il y a de réflexions.
Il faut donc avoir une valeur de l'angle d'incidence i élevée.
La réflexion totale interne engendre très peu de pertes comparée à la réflexion sur un miroir plan.
Dans la pratique, les indices n1 et n2 sont proches (typiquement : 1,46 et 1,48),
ce qui rend l'angle critique proche de 80°, et donc i > 80°.
1. Introduction : 2 types de lentilles
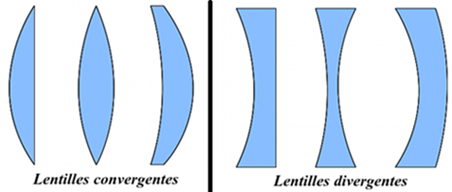
Elles sont largement utilisées dans divers instruments optiques comme les lunettes,
les microscopes et les appareils photo. Le cristallin de l'œil est également une lentille convergente.
On utilise 2 types de lentilles :
-
Les lentilles convergentes :
- Plus épaisses au centre qu'aux bords.
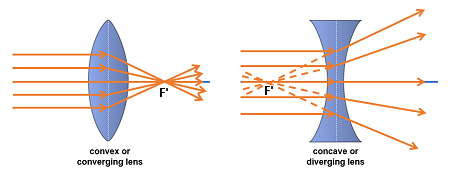
- Convergent les rayons lumineux parallèles vers un point appelé foyer image (F').
- Utilisées pour corriger l’hypermétropie, dans les loupes, etc.
- Plus minces au centre qu'aux bords.
- Divergent les rayons lumineux parallèles, qui semblent provenir d'un point appelé foyer image (F').
- Utilisées pour corriger la myopie.
2. Notations et symboles
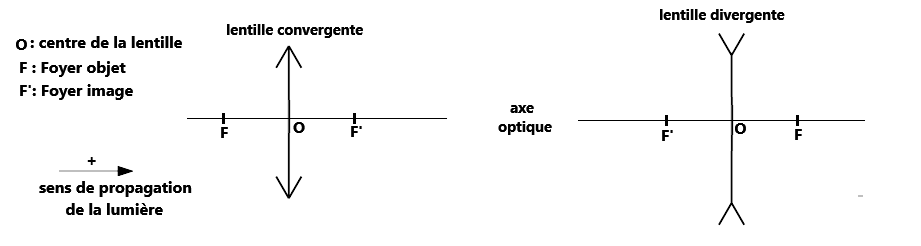
3. 3 rayons pour tracer l'image d'un objet
- Le rayon incident qui passe par le centre de la lentille n'est pas dévié.
- Le rayon incident qui passe par le foyer objet F de la lentille ressort parallèle à l'axe optique.
- Le rayon incident parallèle à l'axe optique ressort en convergeant vers le foyer image F'.
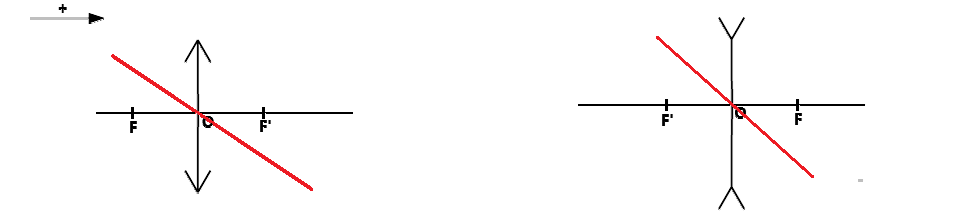
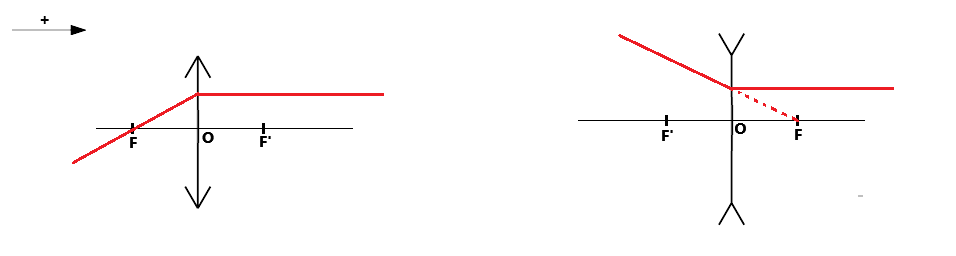
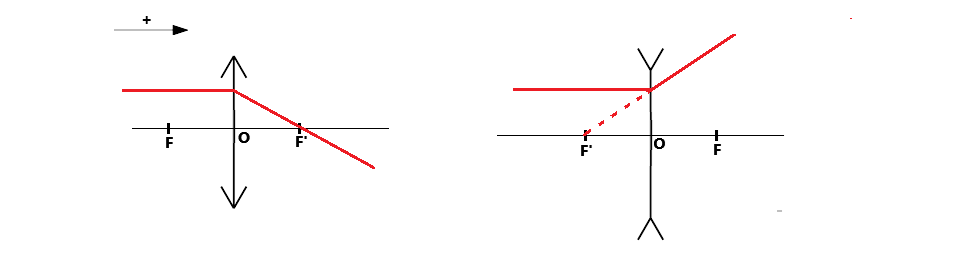
Pour la lentille divergente, on utilise plutôt le rayon qui semble passer par F ou F'.
4. Construire l'image d'un objet par une lentille
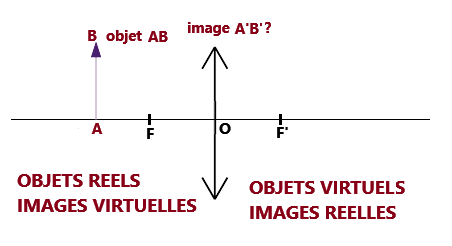
le but est de trouver son image A'B' par construction graphique.
- On se place dans les conditions de Gauss,
c'est-à-dire que les rayons sont peu inclinés par rapport à l'axe optique.
Le système optique est alors stigmate. - A' est forcément sur l'axe optique, donc il suffit de trouver B' pour avoir l'image.
- À gauche de la lentille : les objets sont réels et les images virtuelles.
- À droite de la lentille : les objets sont virtuels et les images réelles.
- Lentille convergente : l'objet est à gauche du foyer objet
- Lentille convergente : l'objet est entre le foyer objet et la lentille
- Lentille divergente : l'objet est à gauche du foyer image
- Le rayon qui semble passer par F ressort parallèle.
- Le rayon parallèle à l'axe optique est dévié, il semble passer par F'.
- Lentille divergente : l'objet est entre F' et la lentille
- Le rayon qui semble passer par F ressort parallèle.
- Le rayon parallèle à l'axe optique est dévié, il semble passer par F'.
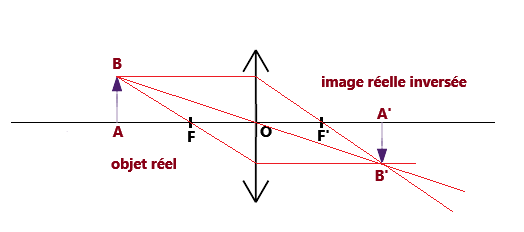
On obtient une image réelle inversée.
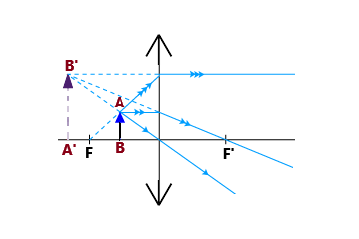
Pour trouver l'image de B, il faut prolonger les rayons lumineux,
car pour un observateur, les rayons lumineux semblent converger à gauche de F.
On obtient une image virtuelle, droite.
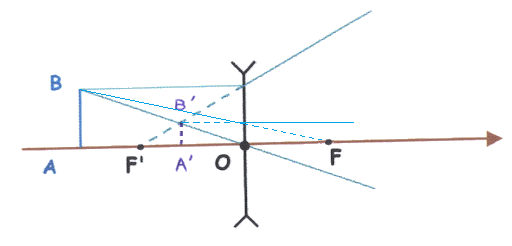
L'image est droite et virtuelle.
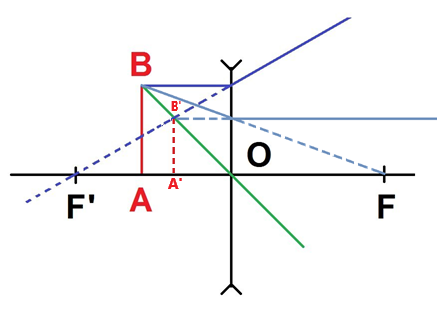
L'image est droite et virtuelle.
5. Et si l'objet est à l'infini...
un immeuble situé à quelques dizaines de mètres est suffisamment éloigné pour être considéré "à l'infini".
Comment représenter les rayons lumineux de tels objets ?
La source se rapproche puis s'éloigne du capteur, l'angle représente l'écart maximum entre les rayons qui arrivent sur le capteur.
Si l'angle est égal à 0, cela signifie que les rayons sont parallèles entre eux, ici l'animation est stoppée à 0.8°.
On constate que les rayons qui nous parviennent d'un objet situé à l'infini sont parallèles.
Ou pas... 😱, l'esprit scientifique consiste aussi à tenir compte du contexte lié à une expérience ou une simulation.
Ici, on a pris une source ponctuelle sur l'axe optique, c'est un cas particulier, mais si la source est décalée ?
Les rayons lumineux d'une source à l'infini restent parallèles entre eux.
Cela rejoint les mathématiques où l'on affirme que les droites parallèles se coupent à l'infini.
Ce qui est intéressant, c'est que les rayons ne sont plus parallèles à l'axe optique.
Les rayons issus de chaque source arrivent sur le capteur avec un angle différent.
Cette différence est appelée diamètre apparent, il dépend de la taille et de la distance (par rapport au capteur) de l'objet lumineux.
Le Soleil a un diamètre apparent très faible (0.5°) car il est très éloigné.
Pour résumer, si je cherche l'image d'une source ponctuelle située à l'infini, on a 2 cas :
- Les rayons de la source sont parallèles à l'axe optique
- Les rayons de la source ne sont pas parallèles à l'axe optique

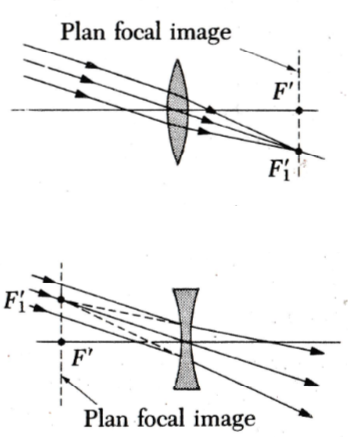
Ce point est appelé foyer secondaire.
Il est situé dans le plan perpendiculaire à l'axe optique et contenant F'.
Il s'agit du plan focal image.
On a bien sûr l'équivalent du côté du foyer objet.