1. Newton's Second Law

Portrait of Isaac Newton
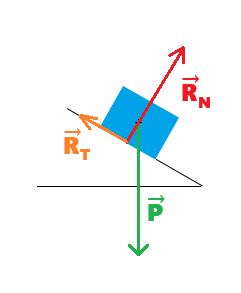
Cube subjected to 3 forces on an inclined plane
Consider a solid object sliding down an inclined plane. We have represented the force balance.
  • System: the solid object
  • Terrestrial reference frame assumed to be inertial
  • The sum of external forces is called the resultant force and is denoted ΣF→
  • In our example, we therefore have: ΣF→ = R→T + R→N + P→
  • The mass of the solid object is denoted m and its acceleration a→

According to Newton's second law: "In an inertial reference frame, the sum of the forces applied to a body
is equal to the product of the mass m of that body and its acceleration."

Thus, ΣF→ = ma→

Let's review the units:

  • The mass m is in kilograms (kg)
  • The acceleration a is in m/s²
  • The resultant force ΣF is in newtons (N)

The unit of force, the newton, is defined as the magnitude of force required to impart
an acceleration of 1 m/s² to a mass of 1 kg: 1 N ≡ 1 kg . m/s²

If the acceleration is zero, we have ΣF→ = 0→, meaning the forces balance each other.
This is Newton's 1st Law (seen in section IV), which is therefore a special case of Newton's 2nd Law.

2. How to Apply Newton's Second Law?

a. A Simple Example

Box pulled horizontally
A box on a horizontal surface is pulled by a string.
Here is the method we can use to apply the 2nd Law of Newton:
  • 1. Choose the system and the reference frame
  • 2. Analyze the forces applied to the system
  • 3. Draw a diagram with the system, the forces, and a→
  • 4. Write ma→ = ΣF→, explicitly stating ΣF→
  • 5. Choose a coordinate system and represent it
  • 6. Project the vector equation onto the axes of the coordinate system
The system is the box, and the reference frame is terrestrial.
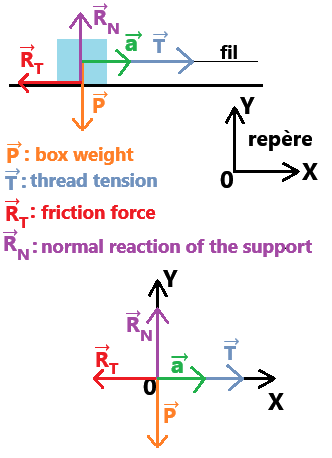
Box pulled horizontally with the force balance

We obtain 4 forces:

  • ΣF→ = R→T + R→N + P→ + T→
  • ma→ = R→T + R→N + P→ + T→
When choosing a coordinate system, the simplest approach is to have axes
that are parallel or perpendicular to the vectors (see diagram).

a→ is necessarily horizontal because the string is pulled horizontally.
To keep things simple, I have represented all vectors starting from the origin of the coordinate system.


The final step is to project the vector equation onto the axes of the coordinate system.
In my coordinate system, the vectors have the following coordinates:

a→(ax, ay), R→T (RTX, RTY), R→N (RNX, RNY), P→ (PX, PY), T→ (TX, TY)
Of course, the coordinates need to be specified. If you have followed section V carefully, you know how to do this. Your turn!

For each vector, click on the 2 correct coordinates.

aX :
aY :
PX :
PY :
TX :
TY :
RNX :
RNY :
RTX :
RTY :
Your equations:
Along the X-axis: m = + + +
Along the Y-axis: m = + + +

By simplifying the zeros, we get:

  • 0 = -P + RN, so P = RN. The weight and the normal reaction balance each other.
  • ma = T - RT
    • If a = 0, then T = RT. The friction and the tension of the wire balance each other.
    • If a < 0, the motion slows down. RT > T, meaning friction is greater than the wire tension.
    • If a > 0, the motion accelerates. T > RT, meaning friction is lower than the wire tension.

b. A Slightly More Complex Example

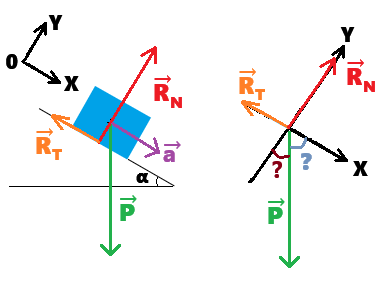
Cube subjected to 3 forces on an inclined plane
Let's revisit the example of the box sliding down an inclined plane.
According to Newton's 2nd Law:
  • ΣF→ = ma→
  • ma→ = R→T + R→N + P→
To utilize this vector relationship, we need to choose a coordinate system and project it onto the axes.
To keep things as simple as possible, we can take the OX axis parallel to the inclined plane.
The (mathematical) challenge is to determine the coordinates of the weight vector.
I have placed the vectors at the origin of the coordinate system.
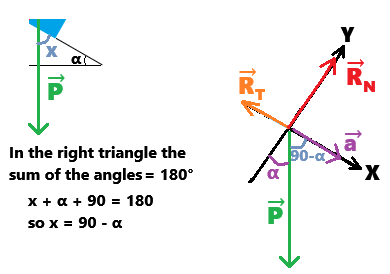
Cube subjected to 3 forces on an inclined plane

The final step is to project the vector relationship onto the axes of the coordinate system.
Hint: 2 useful trigonometric relationships:
  • cos(90 - α) = sinα
  • sin(90 - α) = cosα

For each vector, click on the 2 correct coordinates. Your turn!

aX :
aY :
PX :
PY :
RNX :
RNY :
RTX :
RTY :
Vos équations:
Along the X-axis: m = + +
Along the Y-axis: m = + +

3. Newton's Third Law

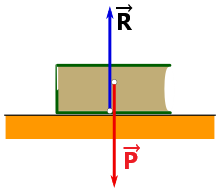
Book resting on a table - Newton's 3rd Law
According to Newton's Third Law, if there is an interaction between two bodies,
the force exerted by body1 on body2 is equal and opposite to the force exerted by body2 on body1.

If we take the example of a book on a horizontal table, according to Newton's 3rd Law:
the two forces balance each other: P→ = - R→ or P→ + R→ = 0→

If the book is stationary or moving at a constant velocity,
according to the principle of inertia (1st Law), we arrive at the same result.
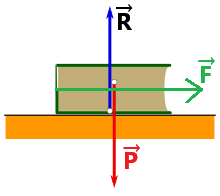
Book resting on a table - Newton's 3rd Law
Imagine that we push this book with a horizontal force F→.
It undergoes accelerated linear motion, so we can no longer apply the principle of inertia.
However, according to Newton's 3rd Law, we can still write: P→ = - R→

Conclusion: Just because we can arrive at the same result using different laws does not mean they are equivalent.