1. La deuxième loi de Newton

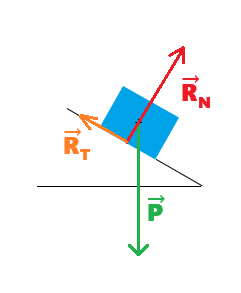
- Système : le solide
- Référentiel terrestre supposé galiléen
- La somme des forces extérieures est appelée force résultante et notée ΣF→
- Dans notre exemple, on a donc : ΣF→ = R→T + R→N + P→
- La masse du solide est notée m et son accélération a→
D'après la deuxième loi de Newton : "Dans un référentiel galiléen, la somme des forces appliquées à un corps
est égale au produit de la masse m de ce corps par son accélération."
Soit ΣF→ = ma→
Faisons le point sur les unités :
- La masse m est en kilogramme (kg)
- L'accélération a est en m/s²
- La résultante des forces ΣF est en newton (N)
L'unité de force, le newton, est définie comme la grandeur de force nécessaire pour imprimer
une accélération de 1 m/s² à une masse de 1 kg : 1 N ≡ 1 kg . m/s²
Si l'accélération est nulle, on a ΣF→ = 0→, les forces se compensent.
C'est la 1ère loi de Newton (vue au IV) qui est donc un cas particulier de la 2ème loi de Newton.
2. Comment exploiter la deuxième loi de Newton ?
a. Un exemple simple
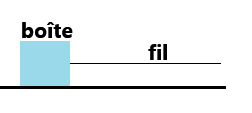
Voici la méthode que l'on peut utiliser pour exploiter la 2ème loi de Newton :
- 1. Choisir le système et le référentiel
- 2. Faire le bilan des forces appliquées au système
- 3. Faire un schéma avec le système, les forces et a→
- 4. Écrire ma→ = ΣF→ en explicitant ΣF→
- 5. Choisir un repère, le représenter
- 6. Projeter la relation vectorielle sur les axes du repère
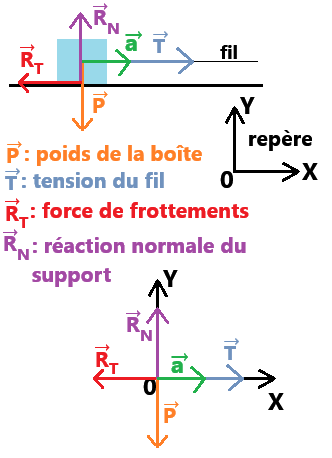
On obtient 4 forces :
- ΣF→ = R→T + R→N + P→ + T→
- ma→ = R→T + R→N + P→ + T→
dont les axes sont parallèles ou perpendiculaires aux vecteurs (voir schéma).
a→ est forcément horizontal, car on tire horizontalement sur le fil.
Pour que ce soit vraiment simple, j'ai représenté tous les vecteurs à partir de l'origine du repère.
La dernière étape consiste à projeter ma relation vectorielle sur les axes de mon repère.
Dans mon repère, les vecteurs ont les coordonnées :
a→(ax, ay), R→T (RTX, RTY), R→N (RNX, RNY), P→ (PX, PY), T→ (TX, TY)
Bien sûr, il faut expliciter les coordonnées. Si vous avez bien suivi la partie V, vous savez le faire. À vous de jouer !
Pour chaque vecteur, il faut cliquer sur les 2 bonnes coordonnées.
En simplifiant les 0, on obtient :
- 0 = -P + RN, soit P = RN. Le poids et la réaction normale se compensent.
- ma = T - RT
- Si a = 0, alors T = RT. Les frottements et la tension du fil se compensent.
- Si a < 0, le mouvement ralentit. RT > T, les frottements sont supérieurs à la tension du fil.
- Si a > 0, le mouvement est accéléré. T > RT, les frottements sont inférieurs à la tension du fil.
b. Un exemple un peu plus compliqué
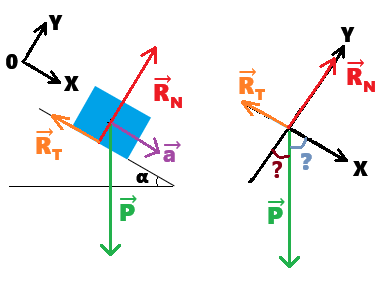
D'après la 2ème loi de Newton :
- ΣF→ = ma→
- ma→ = R→T + R→N + P→
Pour que ce soit le plus simple possible, on peut prendre l'axe OX parallèle au plan incliné.
La difficulté (mathématique) est d'avoir les coordonnées du vecteur poids.
J'ai placé les vecteurs au centre du repère.
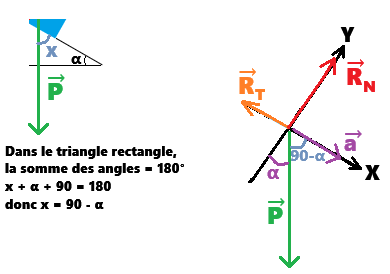
La dernière étape consiste à projeter ma relation vectorielle sur les axes de mon repère.
Aide : 2 relations de trigonométrie utiles :
- cos(90 - α) = sinα
- sin(90 - α) = cosα
Pour chaque vecteur, il faut cliquer sur les 2 bonnes coordonnées. À vous de jouer !
3. La troisième loi de Newton
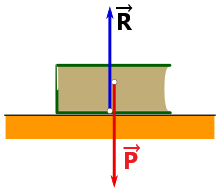
la force du corps1 sur le corps2 est égale et opposée à la force du corps2 sur le corps1.
Si on prend l'exemple d'un livre sur un table horizontale, d'après la 3ème loi de Newton :
les 2 forces se compensent: P→ = - R→ ou P→ + R→ = 0→
d'après le princide d'inertie(1èreloi), on arrive au même résultat.
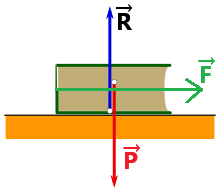
Il a un mouvement rectiligne accéléré, du coup on ne peut plus appliquer le principe d'inertie.
Par contre, d'après la 3ème loi de Newton, on peut toujours écrire : P→ = - R→
Conclusion: ce n'est pas parce qu'on peut arriver au même résultat avec des lois différentes, qu'elles sont équivalentes.