The Motion
Since we can determine Smiley's speed, we can also determine his kinetic energy.
Indeed, the kinetic energy of an object depends only on its mass and speed.
Notations and units:
- Ec: kinetic energy in Joules (J)
- m: mass in kilograms (kg)
- v: in meters per second (m/s)
Formula: Ec = 1/2mv²
2 solids move down an inclined plane, from the point of view of kinetic energy, what is the difference between the 2 movements?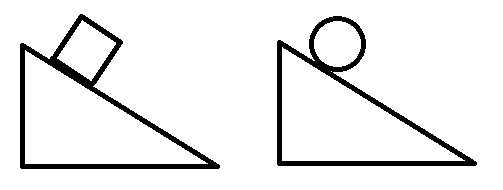
- The cube has a translational movement, its kinetic energy is Ec = 1/2mv²
- The ball has a translational and rotational movement its kinetic energy is Ec = 1/2 mv² + rotational kinetic energy
To summarize, Ec = 1/2mv² represents the kinetic energy of translation.
Smiley has a (random) mass of m = ? kg
Your objectives:
- Click to see the trajectory (click again if you are not satisfied).
- Click on a point of the trajectory
- Calculate the speed at M1 knowing that the time elapsed between 2 red points is ? seconds
- Calculate the corresponding kinetic energy, it should appear in the purple box of SuperCalculator 😁.
(If you are lost )
Reminder about kinetic energy:
Formula: Ec = 1/2mv²
Notations and units:
- Ec: kinetic energy in Joules (J)
- m: mass in kilograms (kg)
- v: in meters per second (m/s)
Just like velocity, we can also distinguish between average acceleration and instantaneous acceleration (a).
Acceleration corresponds to the change in velocity per unit of time (ΔV/Δt):
- a = ΔV/Δt, the difference between average and instantaneous acceleration lies in the value of Δt
if it's sufficiently small, we can speak of instantaneous acceleration. - if t is in seconds (s) and d in meters (m) then V is in m/s and a in m/s² (here, we'll rather use distances in cm)
Let's look at an example instead how to calculate acceleration.
If the acceleration doesn't change, it means the acceleration value is constant.
We're dealing with a special case, it's a uniformly accelerated rectilinear motion
Now let's approach acceleration in the context of a decelerating motion
The acceleration is negative so the velocity decreases, it cancels out and then reverses.
As a result, the smiley starts moving in the opposite direction, because it's a reversible smiley!
And when it starts moving in the opposite direction, it accelerates, so the motion is rectilinearly accelerated.
What does that mean? We've seen that with a decelerating motion the acceleration was negative, has the acceleration become positive?
In fact, no it's just that we need to be more rigorous in studying a motion.
We need an axis associated with a frame of reference (and an origin of time and positions).
Let's say the frame of reference is the gray frame and the Ox axis that gives the origin of positions points towards the positive direction.
Now that I've defined that, we understand better why a negative acceleration will pull the smiley towards the left.
Now,
Smiley can perform either an accelerated or a decelerated motion.
(click again if you're not satisfied.)
Your goal is to obtain the value of acceleration a at M1 in the purple box of SuperCalculator 😁. (If you're lost )
When velocity varies, we can always calculate the average velocity in the same way as in 3. average velocity
What's interesting is to calculate instantaneous velocity.
That is, the velocity at a given instant, during the motion. Alright, but how do we calculate it?
Click on to make the smiley accelerate!
The trick is to think of instantaneous velocity like average velocity but for a very short duration.
We target the point where we want to calculate the instantaneous velocity, we "take" the distance traveled for this short duration,
and apply the formula V = d/Δt as shown below, now,
We will calculate 2 instantaneous velocities at two different points of the trajectory.
Why 2 velocities? It will allow us to calculate the acceleration in 5. acceleration
Click on to make the smiley run and get its trajectory. (click again if you're not satisfied)
Click on 2 different points of the trajectory, at the places where you want to calculate v1 and v2.
Calculating instantaneous velocities v1 and v2 (if you're lost )
- The duration between 2 consecutive points of the trajectory is
- v1 and v2 should appear in the purple boxes of SuperCalculator 😁
In this context, the speed of the smiley is equal to the average speed given by the formula: V = d/Δt.
We will learn how to calculate an average speed step by step:
Step 1: Determine the distance d
- Click on to make the smiley run and get its trajectory. (click again if you're not satisfied)
- To determine the distance d:
- Select the starting point (one of the red points)
- Select the end point
Step 2: Calculate the speed
- Calculate the duration Δt, knowing that between 2 red points the elapsed time is 0.5 seconds
- Using the formula V = d/Δt, calculate the speed V
- The value of V should appear in the purple box of SuperCalculator 😁
- If you are lost, click on , you can start over afterwards.
1. Smiley Race!
But what are these red points? And what are they for?
The runners have left red points at their location at regular time intervals, here, every 0.5 seconds.
We use this method to study motion, we can even calculate speed and acceleration!
Now that we understand the part "1. Description", we can describe the 3 movements:
- 😎: the distance between 2 points increases for the same duration, so the motion is rectilinear and accelerated
- 😊: the distance between 2 points does not change for the same duration, so the motion is rectilinear and uniform
- 🤓: the distance between 2 points decreases for the same duration, so the motion is rectilinear and decelerated
2. Average Speed
By definition, the average speed is the distance traveled divided by the duration of the path.
That is: V = d/Δt
- V: average speed in meters per second (m/s)
- d: distance in meters (m)
- Δt: duration of the path in seconds (s)
I have used the units of the International System (meters and seconds), but any units of time or length are suitable,
you need to adjust the speed unit accordingly. (e.g., if d→km and Δt→h then v→km/h)
We will see in "3. Average Speed" how to calculate this speed.
Motion Description
1. The Trajectory
A trajectory represents the successive positions of the center of gravity of the studied object (called the system) during the movement.
With the trajectory, we can already "partially" describe the motion:
The trajectory is...
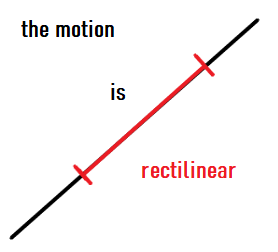
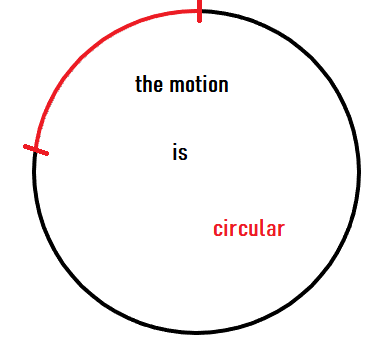

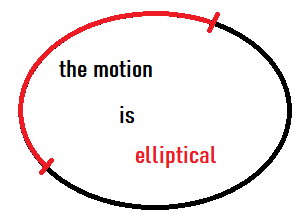

2. Describing Motion with the Trajectory and Speed
If we consider a movement, for the speed, we can consider 3 cases:
- The speed decreases: the motion is slowed down
- The speed remains constant: the motion is uniform
- The speed increases: the motion is accelerated
We can now describe the motion by considering both the trajectory and the speed: