Le mouvement
Puisqu'on est caplable de trouver la vitesse de Smiley, on est aussi capable de déterminer son énergie cinétique.
En effet, l'énergie cinétique d'un objet ne dépend que de sa masse et sa vitesse.
Notations et unités:
- Ec : énergie cinétique en Joule (J)
- m : masse en kilogramme (kg)
- v : en mètre par seconde (m/s)
Formule : Ec = 1/2mv²
2 solides descendent un plan incliné, du point de vu de l'énergie cinétique, quelle est la différence entre les 2 mouvements ?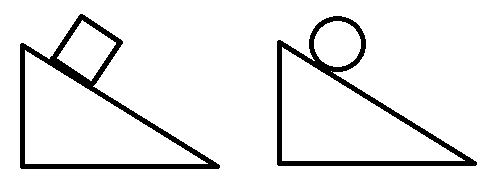
- Le cube a un mouvement de translation, son énergie cinétique est Ec = 1/2mv²
- La boule a un mouvement de translation et de rotation son énergie cinétique est Ec = 1/2mv² + énergie cinétique de rotation
Pour résumer, Ec = 1/2mv² représente l'énergie cinétique de translation.
Smiley a une masse (aléatoire) m = ? kg
Vos objectifs:
- Cliquer sur pour avoir la trajectoire(recliquer si vous n'êtes pas satisfait.)
- Cliquer sur un point de la trajectoire
- Calculer la vitesse en M1 sachant qu'entre 2 points rouges le temps écoulé est de ? seconde
- Calculer l'énergie cinétique correspondante, elle doit apparaître dans la case violette de SuperCalculator 😁.
(Si vous êtes perdus )
Rappel énergie cinétique:
Formule : Ec = 1/2mv²
Notations et unités:
- Ec : énergie cinétique en Joule (J)
- m : masse en kilogramme (kg)
- v : en mètre par seconde (m/s)
Comme pour la vitesse, on peut également distinguer l'accélération moyenne de l'accélération intantanée (a).
L'accélération corespond à la variation de la vitesse par unité de temps (ΔV/Δt) :
- a = ΔV/Δt, la différence entre accélération moyenne et instantanée tient dans la valeur de Δt
si elle est suffisament petite on peut parler d'accélération instantanée. - si t est en seconde (s) et d en mètre (m) alors V est en m/s et a en m/s² (ici, on utilisera plutôt des distances en cm)
Regardons plutôt sur un exemple comment calculer l'accélération.
Si l'accélération ne change pas, ça signifie que la valeur de l'accélération est constante.
On est dans un cas particulier, il s'agit d'un mouvement rectiligne uniformément accéléré
Maintenant abordons l'accélération dans le cadre d'un mouvement ralenti
L'accélération est négative donc la vitesse diminue, elle s'annule puis elle s'inverse.
Du coup, le smiley repart dans l'autre sens, car c'est un smiley réversible!
Et lorsqu'il repart dans l'autre sens, il accélère, donc le mouvement est rectiligne accéléré.
Qu'est-ce à dire? On a vu qu'avec un mouvement ralenti l'accélération était négative, l'accélération est-elle devenue positive?
En fait, non c'est juste qu'il faut être plus rigoureux pour étudier un mouvement.
Il faut un axe associé à un référentiel (et une origine des temps et des positions).
Disons que le référentiel est le cadre gris et l'axe Ox qui donne l'origine des positions pointe vers le sens positif.
Maintenant que j'ai défini ça, on comprends mieux pourquoi une accélération négative va entrainer le smiley vers la gauche.
Maintenant,
Smiley peut nous faire un mouvement accéléré ou ralenti.
(recliquer si vous n'êtes pas satisfait.)
Votre but est d'obtenir la valeur de l'accélération a en M1 dans la case violette de SuperCalculator 😁. (Si vous êtes perdus )
Lorsque la vitesse varie, on peut toujours calculer la vitesse moyenne de la même façon que 3. vitesse moyenne
Ce qui est intéressant, c'est de calculer la vitesse instantanée.
C'est à dire la vitesse à un instant donné, au cous du mouvement. Bon ok, mais comment la calculer?
Cliquer sur pour faire accélérer smiley!
L'astuce, c'est de se dire que la vitesse instantanée est comme une vitesse moyenne mais pour une durée très courte.
On cible le point où l'on veut calculer la vitesse instantanée, on "prend" la distance parcourue pour cette petite durée,
et on applique la formule V = d/Δt comme indiqué ci-dessous, maintenant,
Nous allons calculer 2 vitesses instantanées à deux endroits différents de la trajectoire.
Pourquoi 2 vitesses ? Ca va nous permettra de calculer l'accélération au 5. accélération
Cliquer sur pour faire courir smiley et obtenir sa trajectoire. (recliquer si vous n'êtes pas satisfait)
Cliquer sur 2 points différents de la trajectoires, aux endroits où vous voulez calculer v1 et v2.
Calcul des vitesses instantanées v1 et v2 (si vous êtes perdus )
- La durée entre 2 points consécutifs de la trajectoire est
- v1 et v2 doivent apparaître sur les cases violettes de SuperCalculator 😁
Dans ce contexte, la vitesse du smiley est égale à la vitesse moyenne donnée par la formule : V = d/Δt.
Nous allons apprendre à calculer une vitesse moyenne en procédant par étape :
Etape 1: Déterminer la distance d
- Cliquer sur pour faire courir smiley et obtenir sa trajectoire. (recliquer si vous n'êtes pas satisfait)
- Pour déterminer la distance d:
- Sélectionner le point de départ (un des points rouges)
- Sélectionner le point d'arrivée
Etape 2: Calculer la vitesse
- Calculer la durée Δt, sachant qu'entre 2 points rouges le temps écoulé est de 0.5 seconde
- A partie de la formule V = d/Δt , calculer la vitesse V
- La valeur de V doit apparaître sur la case violette de SuperCalculator 😁
- Si vous êtes perdu cliquer sur , vous pourrez recommencer par la suite.
1. Course de smileys!
Mais c'est quoi ces points rouges ? Et, à quoi ça sert?
Les coureurs ont laissés des points rouges à leur emplacement à intervalle de temps régulier, ici, toutes les 0,5 secondes.
On utilise ce procédé pour étudier le mouvement , on peut même calculer la vitesse et l'accélération!
Maintenant qu'on maîtrise la partie " 1.Description " , on peut décrire les 3 mouvements :
- 😎: la distance entre 2 points augmente pour une durée identique donc le mouvement est rectiligne accéléré
- 😊: la distance entre 2 points ne change pas pour une durée identique donc le mouvement est rectiligne uniforme
- 🤓: la distance entre 2 points diminue pour une durée identique donc le mouvement est rectiligne ralenti
2. La vitesse moyenne
Par définition, la vitesse moyenne est la distance parcourue divisée par la durée du parcours.
Soit : V = d/Δt
- V : vitesse moyenne en mètre par seconde (m/s)
- d : distance en mètre (m)
- Δt : durée du parcours en seconde (s)
J'ai utilisé les unités du système international (mètre et seconde) mais toutes les unités de temps ou de longueur conviennent,
il faut adapter l'unité de la vitesse en conséquence.(exemple : si d→km et Δt→h alors v→km/h)
On verra dans "3. Vitesse moyenne" comment calculer cette vitesse.
1. La trajectoire
Une trajectoire représente les positions successives du centre de gravité de l'objet étudié (appelé système) au cours du déplacement.
Avec la trajectoire, on peut déjà "partiellement" décrire le mouvement:
La trajectoire est ...
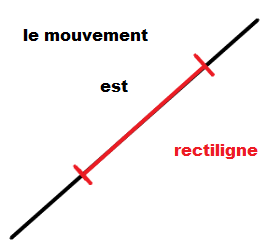
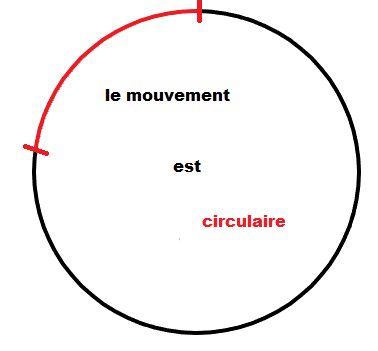

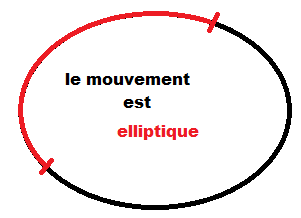
2. La description du mouvement avec la trajectoire et la vitesse
Si on considère un mouvement, pour la vitesse, on peut envisager 3 cas:
- La vitesse diminue : le mouvement est ralenti
- La vitesse reste constant : le monvement est uniforme
- La vitesse augmente : le mouvement est accéléré
On peut maintenant décrire le mouvement en tenant compte de la trajectoire et de la viesse: