Energy
We want to send Smiley into the goal, represented by the green square.
Smiley must reach the square without passing it, meaning it must reach a height h = with zero speed.
If that's the case, Smiley is "captured" and doesn't fall back, otherwise it falls and it's a loss!
What to do? Click (reclick if needed)
Normally, Smiley reached the goal because it was launched vertically into the air with an initial speed v =
How to find the right speed? Just use the conservation of mechanical energy, here's the method:
- a. Define a reference frame, a system, and the studied object
- We choose the Earth's reference frame
- The system: the z-axis with Epp(z=0) = 0J
- The studied system: Smiley
- b. Make a force balance
- Force balance: Smiley's weight
- We neglect air resistance, so Smiley is only subject to its weight
- c. Energies for z = 0
- Kinetic energy: Ec0 = 1/2mv²
- Potential energy: Ep0 = mgz = 0 because z = 0 at the start
- Mechanical energy: Em0 = Ec0 + Ep0 = 1/2mv²
- d. Energies for z = h
- Kinetic energy: Ec1 = 0 because speed v = 0
- Potential energy: Ep1 = mgz = mgh
- Mechanical energy: Em1 = Ec1 + Ep1 = 0 + mgh = mgh
- e. Conservation of mechanical energy:
- Since Smiley is not subject to dissipative forces (air resistance is neglected), mechanical energy is conserved
- Em0 = Em1
- 1/2mv² = mgz
- v² = 2gz (multiply by 2 and divide by m on both sides to isolate v²)
- v = √ (2gz), the maximum height h depends only on the launch speed v.
Select the correct speed and , if you're lost click
The goal is to send Smiley into the goal, represented by the green square.
To help you, you can use the SuperCalculator 😁
Let's throw a Smiley into the air and observe the evolution of kinetic and potential energy!
Click (reclick if needed)
We had the idea to create a third curve.
We get this red curve by adding Ec and Ep.
This is the horizontal line, meaning it's a constant.
It's interesting to have Ec + Ep, this is the mechanical energy denoted as Em.
Thus, Em = Ec + Ep
When the value of Em doesn't change, we say that mechanical energy is conserved.
It is conserved because the system is not subjected to dissipative forces.
Dissipative forces, like friction, reduce the mechanical energy of the system.
For example, if we consider the air friction acting on Smiley,
the mechanical energy gradually decreases over time.
1. Gravitational Potential Energy
The formula for potential energy: Epp = mgz, as seen in part 1, isn't enough. We also need to:
- define a reference frame, i.e., a z-axis for altitude
- set an arbitrary value for Epp at z=0, for example Epp(z=0) = 0J
Examples with images:
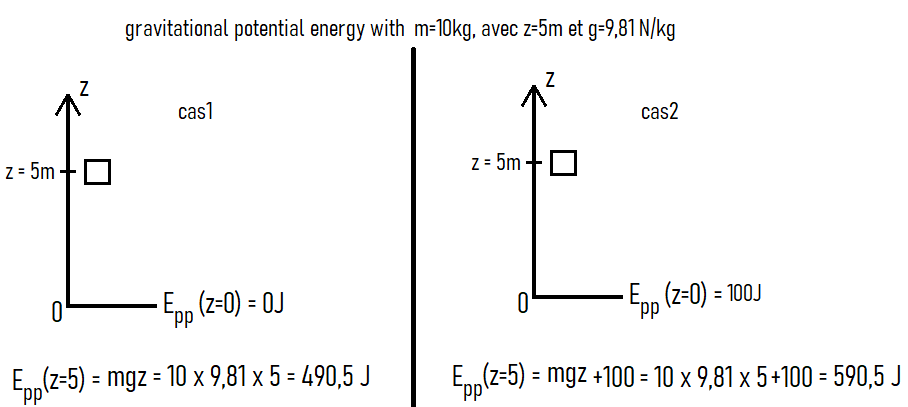
The value of Epp changes according to a constant value (Epp(z=0)) chosen arbitrarily!
Later on, we will see that we will use the variation of Epp (ΔEpp) and ΔEpp doesn't depend on this constant.
We will choose Epp(z=0)=0J to simplify, so this constant doesn't affect the calculations.
To summarize: with the z-axis oriented upwards and Epp(z=0)=0J, Epp = mgz
- m: mass of the studied system in kilograms (kg)
- g: gravitational field strength (g = 9.81 N/kg)
- z: altitude in meters (m)
- Epp: gravitational potential energy in Joules (J)
2. Potential Energy
There are other types of potential energy, for example, if I compress a spring or draw a bow,
we talk about elastic potential energy, denoted as Epel.
If I want to calculate the total potential energy (denoted Ep) of my system, I need to sum them all.
Ep = Epp + Epel + ...
In our study, we will limit ourselves to gravitational potential energy, so Ep = Epp.
A Smiley in free fall?
By definition, an object in free fall is only subject to gravity.
So if I throw a Smiley into the air and ignore air resistance,
it is in free fall: (reclick if you're not satisfied.)
The movement can be divided into two parts:
- The ascent (slowed down straight-line motion):
- The speed decreases until v = 0, and since Ec = 1/2mv²
- the kinetic energy also decreases until Ec = 0
- The descent (accelerated straight-line motion):
- Speed and kinetic energy increase
We are interested in the ascent phase:
Since kinetic energy decreases to 0J, can we say that it disappears?
Since kinetic energy decreases to 0J, can we say that it disappears?
The answer is, of course, no. Energy doesn't disappear, it transforms!
Take the example of an electric heater, the electrical energy supplied doesn't disappear,
it is transformed into heat, i.e., thermal energy.
As Smiley ascends, kinetic energy is transformed into another form of energy.
This "mysterious" energy must:
- increase with altitude (denoted as z in meters (m))
- increase with mass (denoted as m in kilograms (kg))
- depend on Earth's gravity (without weight, Smiley would keep rising indefinitely),
so g is the gravitational field strength (g = 9.81 N/kg)
This is gravitational potential energy, denoted as Epp.
With the formula: Epp = mgz, which we will explain in part 2.