Energie
On veut envoyer Smiley dans le but, représenté par le carré vert.
Le Smiley doit arriver au carré sans le dépasser, c'est à dire arriver à une hauteur h = avec une vitesse nulle.
Si c'est le cas, le Smiley est "capturé" et il ne redescend pas, sinon il redescend et c'est perdu!
Comment faire? Cliquer sur (recliquer si besoin)
Normalement, Le Smiley est arrivé dans le but parcequ'on la lancé verticalement en l'air avec une vitesse initial v =
Comment trouver la bonne vitesse ? Il suffit d'utiliser la conservation de l'énergie mécanique, voici la méthode:
- a. Définir un référentiel, un repère et le système
- On choisit le référentiel Terrestre
- Le repère : l'axe z avec Epp(z=0) = 0J
- Le système étudié : le Smiley
- b. Faire un bilan des forces
- Bilan des forces : le poids du Smiley
- On néglige les frottements de l'air donc le Smiley n'est soumis qu'au poids
- c. Energies pour z = 0
- Energie cinétique: Ec0 = 1/2mv²
- Energie potentielle: Ep0 = mgz = 0 car z = 0 au départ
- Energie mécanique: Em0 = Ec0 + Ep0 = 1/2mv²
- c. Energies pour z = h
- Energie cinétique: Ec1 = 0 car la vitesse v = 0
- Energie potentielle: Ep1 = mgz = mgh
- Energie mécanique: Em1 = Ec1 + Ep1 = 0 + mgh = mgh
- d. Conservation de l'énergie mécanique:
- Puisque le Smiley n'est pas soumis à des forces dissipatives (on néglige les frottements), l'énergie mécanique se conserve
- Em0 = Em1
- 1/2mv² = mgz
- v² = 2gz (on multiplie par 2 et on divise par m de chaque côté pour isoler v²)
- v = √ (2gz) , la hauteir maximale h, ne dépend que la vitesse v à laquelle le smiley est lancé.
Sélectionner la bonne vitesse et , si vous êtes perdu cliquer sur
L'objectif est d'envoyer Smiley dans le but, représenté par le carré vert.
Pour vous aider vous pouvez utiliser le SuperCalculator 😁
Lançons un Smiley en l'air et regardons l'évolution de l'énergie cinétique et potentielle !
Cliquez sur (recliquer si besoin)
On a eu l'idée de faire une 3ème courbe.
On obtient cette courbe rouge en additionnant Ec et Ep.
C'est la droite horizontale, c'est à dire une constante.
Il est intéressant d'avoir Ec + Ep, c'est l'énergie mécanique noté Em.
Donc Em = Ec + Ep
Lorsque la valeur de Em ne varie pas, on dit que l'énergie l'énergie mécanique se conserve.
Elle se conserve car le système n'est pas soumis à des forces dissipatives.
Les forces dissipatives comme les frottements diminuent l'énergie mécanique du système.
Par exemple, si on tient compte des forces de frottements du Smiley dans l'air,
l'énergie mécanique diminue lentement au cours du temps.
1. Energie potentielle de pesanteur
La formule de l'énergie potentielle : Epp = mgz, vu dans la partie 1 n'est pas suffisante, il faut:
- définir un repère, c'est à dire un axe z pour l'altitude
- définir une valeur arbitraire de Epp pour z=0 ,par exemple Epp(z=0) = 0J
Des exemples en images :
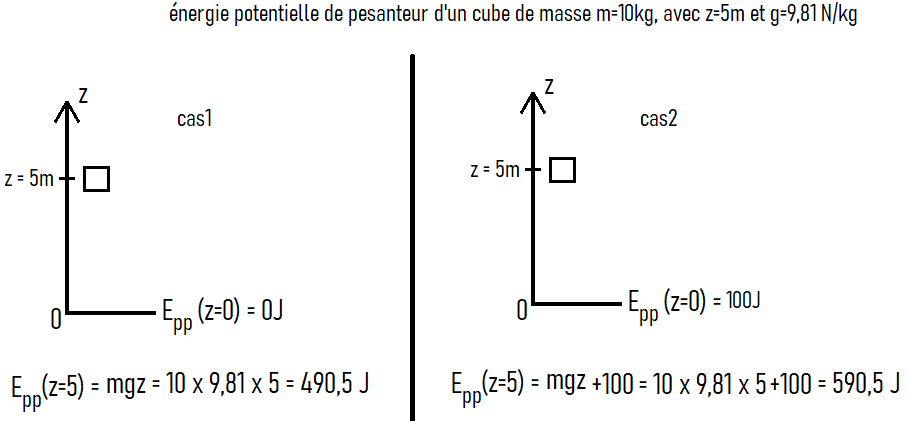
La valeur de Epp, change selon une valeur constante (Epp(z=0)) choisie de manière arbitraire!
On verra plus tard, qu'on utilisera la variation de Epp (ΔEpp) et ΔEpp ne dépend pas de cette constante.
On choisira Epp(z=0)=0J pour simplifier, du coup la valeur de cette constante n'intervient pas dans les calculs.
Pour résumer : avec un axe des z orienté vers le haut et Epp(z=0)=0J, Epp = mgz
- m : masse du système étudié en kilogramme(kg)
- g : intensité du champ de pesanteur (g = 9,81 N/kg)
- z : altitude en mètre(m)
- Epp : énergie potentielle de pesanteur en Joule(J)
2. Energie potentielle
Il existe d'autres énergies potentielles, par exemple si je compresse un ressort ou si je bande un arc,
on parle d'énergie potentielle élastique que l'on peut noter Epel
Si je veux calculer l'énergie potentielle (notée Ep) totale de mon système, il faut que je les additionne toutes.
Ep = Epp + Epel + ...
Dans le cadre de notre étude, on se limitera à l'énergie potentielle de pesanteur donc Ep = Epp.
Un Smiley en chute libre ?
Par définition, un objet en chute libre n'est soumis qu'au poids.
Donc si je lance un Smiley en l'air et que je néglige les forces de frottements de l'air,
il est en chute libre : (recliquer si vous n'êtes pas satisfait.)
Le mouvement peut se décomposer en 2 parties:
- La montée (rectiligne ralenti):
- La vitesse diminue jusqu'à v = 0, et puisque Ec = 1/2mv²
- l'énergie cinétique diminue également jusqu'à Ec = 0
- La descente (rectiligne accéléré):
- La vitesse et l'énergie cinétique augmentent
On s'intéresse à la phase de montée:
Puisque l'énergie cinétique diminue jusqu'à 0J, peut-on dire qu'elle disparaît?
Puisque l'énergie cinétique diminue jusqu'à 0J, peut-on dire qu'elle disparaît?
La réponse est bien sûr non, l'énergie ne disparaît pas, elle se transforme!
Prenons l'exemple d'un radiateur électrique, l'énergie électrique fournie ne disparaît pas,
elle est transformée en chaleur, c'est à dire en énergie thermique.
Lorsque Smiley monte, l'énergie cinétique se transforme en une autre énergie.
Cette "mystérieuse" énergie doit:
- augmenter avec l'altitude (noté z en mètre(m))
- augmenter avec la masse (noté m en kilogramme(kg))
- dépendre de l'attraction terrestre (sans poids Smiley continuerait à monter indéfiniment)
soit g l'intensité du champ de pesanteur (g = 9,81 N/kg)
Il s'agit de l'énergie potentielle de pesanteur, que l'on peut noter Epp.
Avec la formule : Epp = mgz, que l'on précisera dans la 2ème partie.